теплоемкость имеет определенное числовое значение и является однозначной характеристикой тепловых свойств вещества тела. Важнейшими являются молярные теплоемкости при постоянном объеме и постоянном давлении. Именно они приводятся в таблицах. Для этих величин из (4) получим следующие соотношения:
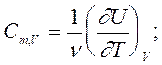 (5)
(5)
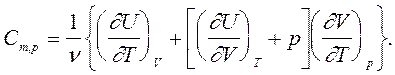 (6)
(6)
Для любых твердых и жидких веществ различие между значениями Cm,V и Cm,p несущественно (сравнительно мало объемное расширение (¶V/¶T) этих веществ), а для газов оно значительно.
![]() Найдем
молярные теплоемкости идеального газа. Внутренняя энергия идеального газа - это
энергия теплового движения молекул и атомов в молекулах. Она слагается из кинетической
энергии центра масс молекулы, кинетической энергии ее вращения и энергии
колебаний атомов. Согласно закону равнораспределения энергии по степеням свободы,
на каждую степень свободы молекулы приходится в среднем энергия равная kT/2, где k - постоянная
Больцмана. Если молекула имеет i степеней
свободы, то средняя энергия теплового движения, приходящаяся на одну молекулу,
равна <e>=ikT/2. Тогда
внутренняя энергия идеального газа, содержащего N
молекул
Найдем
молярные теплоемкости идеального газа. Внутренняя энергия идеального газа - это
энергия теплового движения молекул и атомов в молекулах. Она слагается из кинетической
энергии центра масс молекулы, кинетической энергии ее вращения и энергии
колебаний атомов. Согласно закону равнораспределения энергии по степеням свободы,
на каждую степень свободы молекулы приходится в среднем энергия равная kT/2, где k - постоянная
Больцмана. Если молекула имеет i степеней
свободы, то средняя энергия теплового движения, приходящаяся на одну молекулу,
равна <e>=ikT/2. Тогда
внутренняя энергия идеального газа, содержащего N
молекул
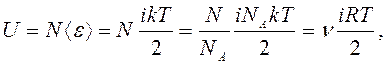 (7)
(7)
где NA - постоянная Авогадро; R - молярная (универсальная) газовая постоянная.
Согласно (7), внутренняя энергия идеального газа не зависит от объема. Это естественное следствие модели идеального газа, в которой потенциальной энергией межмолекулярного взаимодействия пренебрегают.
Из (7) следует,что 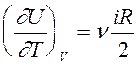 и
и 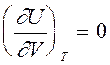 .
Тогда для идеального газа в соответствии с (5) и (6) получим
.
Тогда для идеального газа в соответствии с (5) и (6) получим
Cm,V=iR/2, (8)
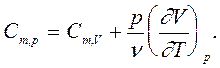 (9)
(9)
Из уравнения Менделеева-Клапейрона:
pV = nRT (10)
определим второе слагаемое в (9):
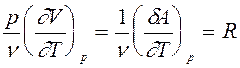 (11)
(11)
Таким образом,
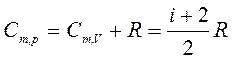 . (12)
. (12)
Это соотношение называется уравнением Майера.
Физический смысл молярной газовой постоянной R вытекает из (11): она равна работе, совершаемой одним молем газа при изобарическом повышении его температуры на один кельвин.
Отношение теплоемкостей
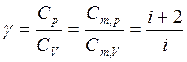 (13)
(13)
определяется только числом степеней свободы молекулы газа и играет большую роль в молекулярной физике. Значение g для разных газов различно.
Для определения теплоемкостей газов опытным путем было предложено много различных методов, которые дают возможность измерять C m,p и отношение C m,p/ C m,V, т.е. величину g.
1.Калориметрический метод. Для измерения C m,p нагретый газ заставляют под постоянным давлением протекать по змеевику, погруженному в калориметр, которому газ отдает свою теплоту. Так как при этом можно пропустить по змеевику значительное количество газа, то измерения C m,p можно произвести с большой точностью. Величину C m,V можно вычислить, если известно отношение теплоемкостей g.
2. Электрические методы определения удельных теплоемкостей газов основаны на непосредственном измерении при помощи термоэлементов изменения электрического сопротивления, возникающего в термоэлементах при изменении температуры. Электрические методы применяются как для определения C m,p, так и C m,V.
3. Метод адиабатического расширения (метод Клемана - Дезорма) применяется только для определения g = C m,p/ C m,V.
4. Метод акустический, основанный на применении формулы Лапласа служит также для определения g.
В данной работе мы рассмотрим метод адиабатического расширения.
Теория метода. Возьмем большой сосуд «А» (рис.1), наполненный воздухом. При помощи насоса в этот сосуд накачивается воздух до некоторого давления, избыток которого над атмосферным давлением можно определить по манометру
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.