Лекция 7. КОЛЕБАНИЯ. УРАВНЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА.

Колебательным называется процесс, при котором какая-либо величина последовательно отклоняется то в одну, то в другую сторону от некоторого своего среднего значения.

Механической колебательной системой называется совокупность тел, в которой могут происходить колебательные процессы. Такая система имеет положение устойчивого равновесия!
![]()
например


пружинный маятник - математический маятник -
модель колебательной системы идеал. система, состоящая из матер. точки
состоящей из пружины жесткостью k массой m, подвешенной на невесомой
и тела массой m нерастяж нити, колеб. под действие силы
тяжести.
|

Свободными (собственными) называются колебания, возникшие в колебательной системе после однократного выведения ее из положения равновесия и происходящие только под действием внутренних сил, при отсутствии сил сопротивления движению.
Колебания горизонтального пружинного маятника.
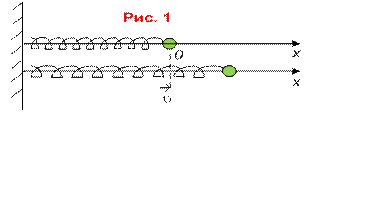 Задача: описать движение
тела под действием упругой и квазиупругой силы (т. е. модуль силы
пропорционален смещению).
Задача: описать движение
тела под действием упругой и квазиупругой силы (т. е. модуль силы
пропорционален смещению).

 а) динамическая
модель: по II з. Ньютона
а) динамическая
модель: по II з. Ньютона 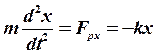 ,
обозначим
,
обозначим 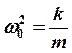 (1)
(1)
![]()

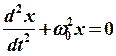 (2) диф. уравнение движения решение:
(2) диф. уравнение движения решение: ![]() (3)
(3)

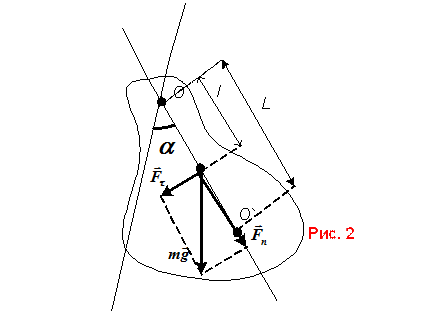 Колебания физического маятника. Задача: описать
колебания АТТ под действием
Колебания физического маятника. Задача: описать
колебания АТТ под действием ![]()

![]()
![]() или
или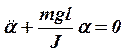 ,
считая
,
считая 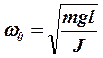 , то
, то![]() ,
решение
,
решение ![]() .
.
Приведенная длина 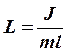

Гармоническими называются колебания, совершаемые под
действием упругой (квазиупругой) силы, при которых какая-либо величина
изменяется с течением времени по закону косинуса или синуса ![]() ,
,![]() (4).
(4).

Смещением хt или уt называется любое отклонение физической величины от ее значения в положении равновесия.
![]()
Амплитудой А называется максимальное смещение.
![]()
Фазой колебания называется
аргумент синуса или косинуса ![]() .
.

Циклическая или круговая частота: 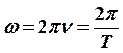

![]() - начальная фаза колебания -
характеризует смещение в момент начала отсчета времени.
- начальная фаза колебания -
характеризует смещение в момент начала отсчета времени.
 Периодом Т называется
промежуток времени, в течение которого совершается одно полное колебание.
Периодом Т называется
промежуток времени, в течение которого совершается одно полное колебание.
 Частота
колебаний – величина, обратная периоду
Частота
колебаний – величина, обратная периоду 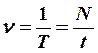

Гармоническим осциллятором называется система, совершающая гармонические колебания.
б) кинематическая модель: при движении материальной
точки по окружности с постоянной по модулю скоростью проекция радиуса-вектора
точки на ось 0х:![]() , где амплитуда равна
модулю радиуса-вектора точки А=
, где амплитуда равна
модулю радиуса-вектора точки А=![]() .
.
 |
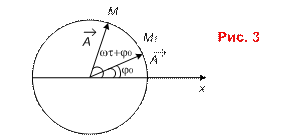
х - проекция радиуса-вектора ![]() на ось 0х.
на ось 0х.

![]() Проекции: мгновенной скорости:
Проекции: мгновенной скорости:
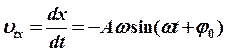 (5),
(5),
 мгновенного ускорения:
мгновенного ускорения: 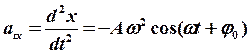 (6).
(6).
![]()

![]() в) энергия
колебаний: кинетическая
в) энергия
колебаний: кинетическая 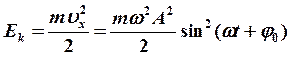
 потенциальная
потенциальная 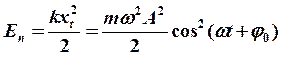 .
.
![]()


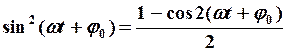
Полная энергия колебаний 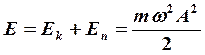 (7)
- пропорциональна амплитуде А2.
(7)
- пропорциональна амплитуде А2.
При отсутствии внешних сил ![]() или
когда сумма проекций внешних сил на направление колебаний
или
когда сумма проекций внешних сил на направление колебаний ![]() , выполняется закон сохранения механической
энергии гармонического осциллятора (пружинного маятника):
, выполняется закон сохранения механической
энергии гармонического осциллятора (пружинного маятника):

![]() ,
, 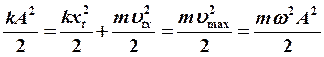
Для собственных колебаний пружинного маятника (из этого закона) циклическая
 частота
частота 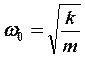 ,
период собственных колебаний
,
период собственных колебаний 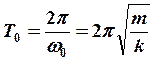
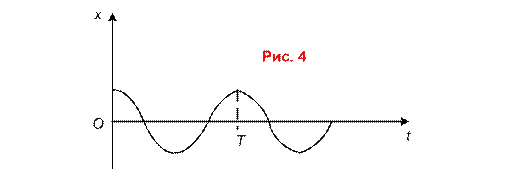
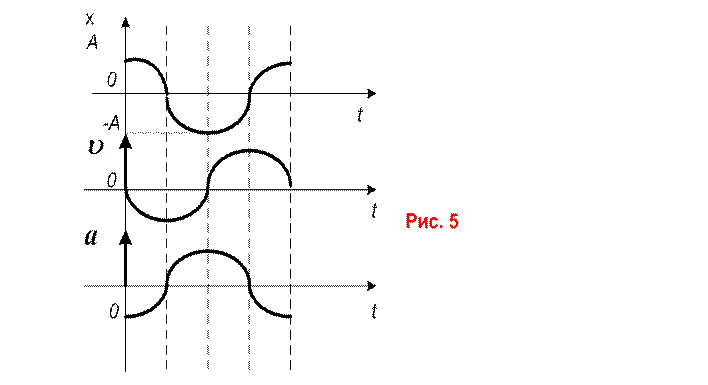
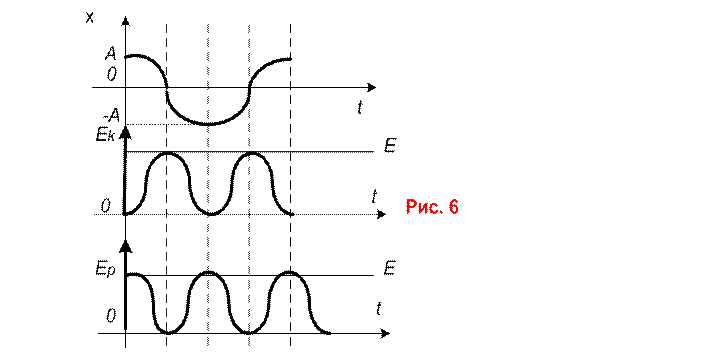
 Графическое
представление колебаний.
Графическое
представление колебаний.
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ
 - наиболее просто осуществляется методом
векторных диаграмм. В этом случае рассматривается кинематическая модель
колебаний - зависимость от времени проекции радиуса-вектора (вектора
амплитуды) точки, вращающегося с постоянной угловой скоростью.
- наиболее просто осуществляется методом
векторных диаграмм. В этом случае рассматривается кинематическая модель
колебаний - зависимость от времени проекции радиуса-вектора (вектора
амплитуды) точки, вращающегося с постоянной угловой скоростью.
![]()
![]()
![]()
![]()
сложение колебаний одной частоты, происходящих вдоль одного направления
(одна степень свободы).
![]()
![]() (8) -
амплитуда результирующего колебания.
(8) -
амплитуда результирующего колебания.

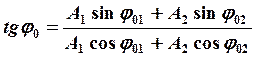 (9)
– начальная фаза результирующего колебания.
(9)
– начальная фаза результирующего колебания.
2) сложение колебаний одной частоты, происходящих во взаимно перпендикулярных направлениях (две степени свободы)
![]()
 а) при одинаковых
частотах и фазах колебаний
а) при одинаковых
частотах и фазах колебаний ![]() сложение колебаний
вдоль оси 0х
сложение колебаний
вдоль оси 0х ![]() и вдоль оси 0у
и вдоль оси 0у
![]() дает результирующее колебание, при
котором в любой момент
дает результирующее колебание, при
котором в любой момент 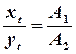 , т.е. результирующее
колебание происходит, например, вдоль прямой СС1 по закону:
, т.е. результирующее
колебание происходит, например, вдоль прямой СС1 по закону:

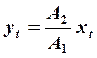 - линейно
поляризованное колебание, где
- линейно
поляризованное колебание, где 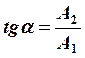 - тангенс угла
наклона СС1 к оси 0х.
- тангенс угла
наклона СС1 к оси 0х.


![]() Если
Если ![]() , то
, то 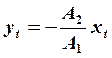 -
это также линейно поляризованное колебание вдоль прямой, тангенс угла
наклона которой к оси 0х равен
-
это также линейно поляризованное колебание вдоль прямой, тангенс угла
наклона которой к оси 0х равен 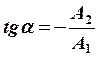

 б) при
б) при ![]() и разности фаз
и разности фаз 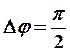 слагаемые
колебания
слагаемые
колебания ![]() и
и 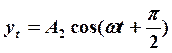 и результирующее колебание называется эллиптически
поляризованным т.к.
и результирующее колебание называется эллиптически
поляризованным т.к. 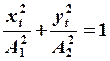 , (Аналогично в случае разности фаз колебаний
, (Аналогично в случае разности фаз колебаний 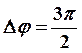 ).
).
 |
в) при иной разности фаз колебаний, траекторией точки также будет эллипс, но его оси не будут параллельными осям 0х и 0у.
г) если частоты слагаемых колебаний различны, то результирующее движение точки, в общем случае, очень сложное и непериодическое.

Но если частоты слагаемых колебаний ![]() и
и ![]() относятся
друг к другу как целые числа, то результирующее движение точки повторяется
через равные отрезки времени, содержащие по целому, хотя и неодинаковому числу
периодов как одного, так и другого слагаемых колебаний.
относятся
друг к другу как целые числа, то результирующее движение точки повторяется
через равные отрезки времени, содержащие по целому, хотя и неодинаковому числу
периодов как одного, так и другого слагаемых колебаний.

Фигурами Лиссажу называются неизменные во времени
траектории движения точки, образующиеся при целочисленных отношениях частот ![]() и
и ![]() слагаемых
взаимно перпендикулярных колебаний.
слагаемых
взаимно перпендикулярных колебаний.
На рисунках фигуры Лиссажу при ![]() ,
, ![]() ,
,![]() .
.
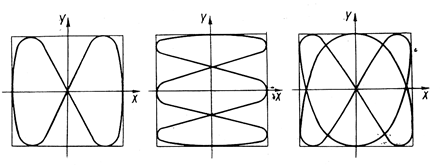
Рис. 9
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.