Таким образом, теплопроводность твердых тел в подавляющем большинстве случаев обусловлена двумя механизмами: движением электронов проводимости (электронная теплопроводность, æэл) и тепловыми колебаниями атомов и молекул твердого тела (фононная теплопроводность, æф). Первый механизм доминирует в металлах, второй определяет теплопроводность неметаллов. В некоторых полупроводниках, полуметаллах и сильно разупорядоченных сплавах оба механизма дают сравнимые вклады в теплопроводность.
Из выше сказанного следует, что суммарная теплопроводность твердого тела определяется формулой
![]() ,
(16) где
,
(16) где ![]() – электронная теплопроводность,
– электронная теплопроводность,
![]() – фононная теплопроводность.
– фононная теплопроводность.
Для металлов и сплавов теплопроводность можно оценить, используя закон Видемана – Франца:
![]() , (17)
, (17)
где 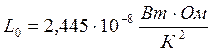 – число Лоренца,
– число Лоренца,
![]() – электропроводность,
– электропроводность, ![]() ,
,
![]() – температура, К.
– температура, К.
Подобное соотношение было впервые установлено учеными Видеманом и Францем и поэтому носит их имя. Важность формулы (17) в том, что она показывает связь теплопроводности с электропроводностью.
Для большинства металлов и сплавов закон Видемана – Франца справедлив при высоких и близких к абсолютному нулю температурах. Для чистых металлов в области промежуточных тимператур этот закон дает завышенные значения æ. Для сплавов он дает заниженные значения теплопроводности (до 10 раз при температурах около 20К для сильно разупорядоченных многокомпонентных сплавов).
Теория метода
Найдем коэффициент теплопроводности металлического стержня цилиндрической формы. Пусть один его конец поддерживается при большей температуре, чем другой.
Плотность теплового потока от нагретого торца
стержня к холодному для одномерного случая выражается формулой (11). Считая,
что температура зависит только от одной координаты ![]() , из уравнения (11) получаем, что плотность
теплового потока равна
, из уравнения (11) получаем, что плотность
теплового потока равна
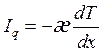 .
(18)
.
(18)
По определению, плотность теплового потока – это количество теплоты, проходящее в единицу времени через единицу площади поверхности:
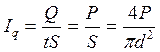 ,
(19)
,
(19)
где ![]() – количество теплоты, сообщаемое стержню;
– количество теплоты, сообщаемое стержню;
![]() – время прохождения тепла через стержень;
– время прохождения тепла через стержень;
![]() – площадь поперечного сечения стержня;
– площадь поперечного сечения стержня;
![]() – мощность источника теплоты;
– мощность источника теплоты;
![]() – диаметр стержня.
– диаметр стержня.
Поскольку распространение
тепла по стержню рассматривается на расстояниях много меньше линейных размеров
самого стержня, изменение температуры на единицу длины стержня ![]() в формуле (18) можно представить, как
в формуле (18) можно представить, как
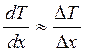 ,
(20)
,
(20)
где ![]() – изменение температуры;
– изменение температуры;
![]() – расстояние, на котором
температура изменяется на
– расстояние, на котором
температура изменяется на ![]() .
.
Тогда, подставляя (19) и (20) в (18), и, учитывая, что знак “–“ выражает направление переноса тепла от области с большей температурой к области с меньшей температурой, тогда как градиент направлен в сторону возрастания этой величины, получим, что коэффициент теплопроводности стержня равен
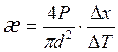 ,
(21)
,
(21)
где ![]() – мощность источника теплоты;
– мощность источника теплоты;
![]() – диаметр стержня;
– диаметр стержня;
![]() – изменение температуры;
– изменение температуры;
![]() – расстояние, на котором температура
изменяется на
– расстояние, на котором температура
изменяется на ![]() .
.
Кроме того в реальных условиях необходимо учитывать достаточно интенсивный теплообмен стержня с окружающей средой, который имеет место, несмотря на используемую в лабораторной установке теплоизоляцию стержня. В итоге формула (21) примет вид
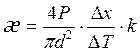 ,
(22)
,
(22)
где
![]() – коэффициент,
учитывающий теплообмен натревателя и стержня с окружающей средой.
– коэффициент,
учитывающий теплообмен натревателя и стержня с окружающей средой.
Для установки, используемой в работе, коэффициенты, учитывающие теплообмен стержня с окружающей средой, соответствующие случаям измерения разности температур между точками стержня
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.