Построение поля корреляции. Оценка статистической надежности результатов регрессионного моделирования с помощью F-критерия Фишера и t-критерия Стьюдента

Оценим с помощью t-критерия Стьюдента параметры уравнений регрессии при  и . Значения  рассчитываются по формулам:

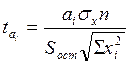
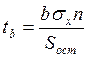
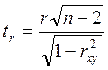
Определим табличное значение t-критерия Стьюдента при  и числе степеней свободы 16-2=14:

Определим табличное значение t-критерия Стьюдента при  и числе степеней свободы 16-2=14:

Рассчитанные значения :

При  признается незначимость критерия, при  признается значимость критерия;

Из рассмотренных уравнений регрессии наилучшим следует считать уравнение регрессии в виде многочлена третьей степени, т.к. для этого уравнения максимальны значения коэффициентов корреляции и детерминации, это уравнение является гомоскедастичным, это уравнение является статистически значимым и надежным.

5  Определение прогнозного значения результата:

Произведем  прогноз значения среднего размера пенсий, если прогнозное значение уровня прожиточного минимума увеличится на 6% от среднего уровня, т.е. составит 5098,6 рублей.

Используя уравнение регрессии в виде многочлена третьей степени находим величину среднего размера пенсий: рублей.

Значение коэффициента t находим по таблице распределения Стьюдента для уровня значимости 5 % и числа степеней свободы равного 14 t=2,15.

Значение коэффициента t находим по таблице распределения Стьюдента для уровня значимости 1 % и числа степеней свободы равного 14 t=2,98.

Вычислим необходимые коэффициенты:

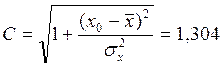
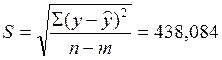
Для уровня значимости 5 %:

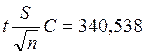
Следовательно, с вероятностью 95% можно утверждать, что если значение прожиточного минимума будет составлять 5098,6, то значение среднего размера пенсий будет находится в интервале:, т.е. .

Таким образом, учитывая «остаточную» вариацию результативного признака в данной выборке, можно полагать с вероятностью 95%, средний размер пенсий при уровне прожиточного минимума в 5098,6 рублей будут не меньше 6325,955 рублей и не больше 7007,032 рублей.

Для уровня значимости 1 %:

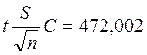
Следовательно, с вероятностью 99% можно утверждать, что если значение прожиточного минимума будет составлять 5098,6, то значение среднего размера пенсий будет находится в интервале:, т.е. .

Таким образом, учитывая «остаточную» вариацию результативного признака в данной выборке, можно полагать с вероятностью 99%, средний размер пенсий при уровне прожиточного минимума в 5098,6 рублей будут не меньше 6194,491 рублей и не больше 7138,496  рублей.

В первом случае (т.е. для вероятности 95 %) доверительный интервал уже, т.к. допустимо более высокое отклонение фактического результата от расчетного.

6 Оценка полученных результатов:

Из рассмотренных уравнений регрессии наилучшим следует считать уравнение регрессии в виде многочлена третьей степени, т.к. для этого уравнения максимальны значения коэффициентов корреляции и детерминации, это уравнение является гомоскедастичным, это уравнение является статистически значимым и надежным. Уравнение регрессии в виде многочлена третьей степени имеет вид

Связь между переменными сильная. Уравнение регрессии объясняет 46,2% дисперсии результативного фактора, а на долю прочих факторов приходится 53,8% ее дисперсии.

С вероятностью 95% можно утверждать, средний размер пенсий при уровне прожиточного минимума в 5098,6 рублей будут не меньше 6194,491 рублей и не больше 7138,496  рублей. С вероятностью 99% можно утверждать, средний размер пенсий при уровне прожиточного минимума в 5098,6 рублей будут