Построение поля корреляции по данным таблицы и формулирование гипотезы о форме связи. Расчет параметров уравнений парных регрессии. Оценка тесноты связи с помощью показателей корреляции и детерминации

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

«Комсомольский-на-Амуре государственный

Технический университет»

расчетно-графическое задание

по  эконометрике

Студент группы 8ФК3ка-2                                                                     А.Э. Явор

Преподаватель                                                                                      Д.Н. Кузнецов

2011
Содержание:

1. Условия задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

2. Решение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . .  . . . . . . . . . . . . . . . . .  5

3. Список использованных источников . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  14

Задача:

По некоторым территориям России известны данные, приведенные в таблице 1:    Таблица 1

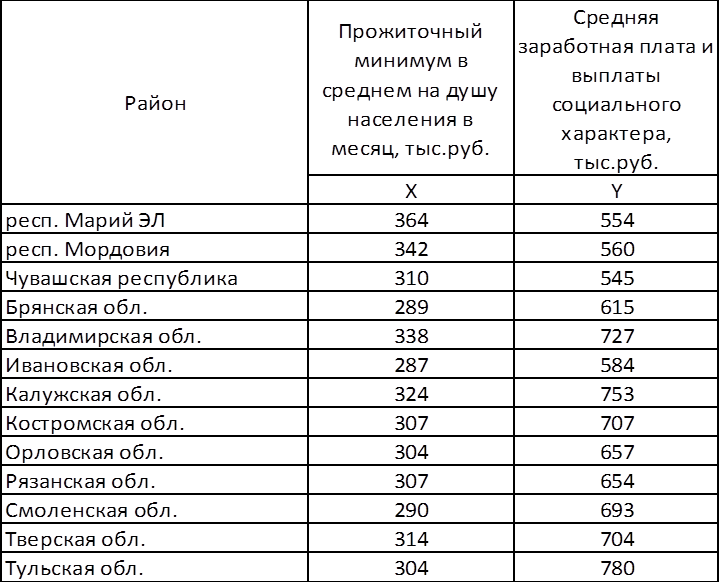
1)  Построить поле корреляции по данным таблицы 1 и сформулировать гипотезу о форме связи.

2) Рассчитать параметры уравнений парных регрессии:

          Линейной;

          Степенной;

          Логарифмической;

          Показательной.

3) Оценить тесноту связи с помощью показателей корреляции и детерминации.

4) Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в п.3 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

5) Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7 % от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости  α=0,05.

Решение:

1)  Построить поле корреляции по данным таблицы 1 и сформулировать гипотезу о форме связи:

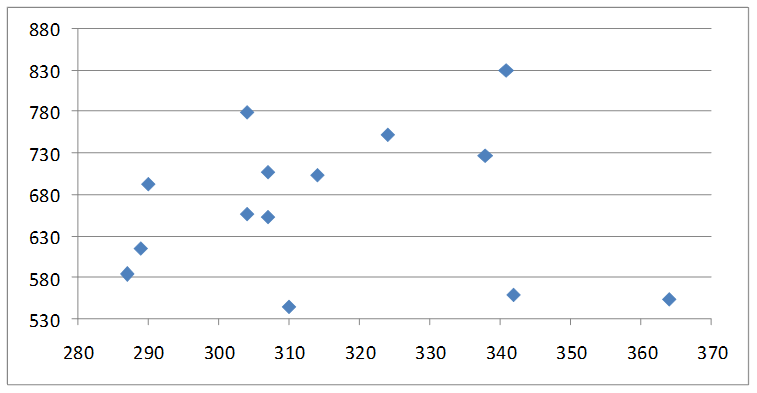
Рис. 1.1  Поле корреляции по данным таблицы 1.

2) Рассчитать параметры уравнений парных регрессии:

          Линейной;

          Степенной;

          Логарифмической;

          Показательной.

а)  Линейная парная регрессия рассчитывается по формуле:  ŷ = a+ b∙ x.

Для расчета параметров  a и b линейной регрессии  ŷ = a+ b∙ xиспользуем формулы:  ;    .

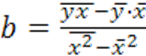В таблице 2 рассчитаем средние величины значений  x и y

                                                                                          Таблица 2

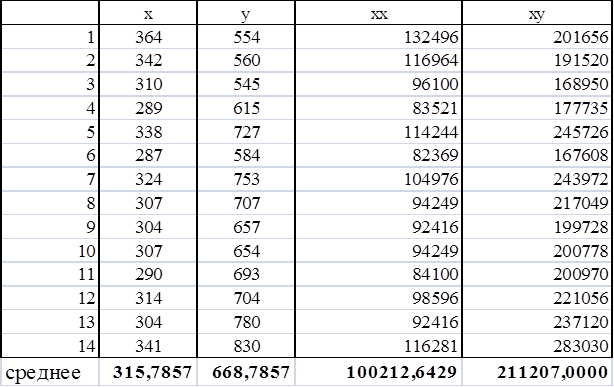
  Вычислим значение коэффициента регрессии b:

 b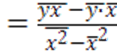 = (211207 – 668,7857∙315,7857)/100212,6429 – 315,7857∙315,7857) =

= 0,029.

   Отсюда   a =  = 668,7857 – 0,029∙315,7857 = 659,7840.

Следовательно, линейное уравнение регрессии будет выглядеть следующим образом:  ŷ = 659,7840 + 0,029 x.

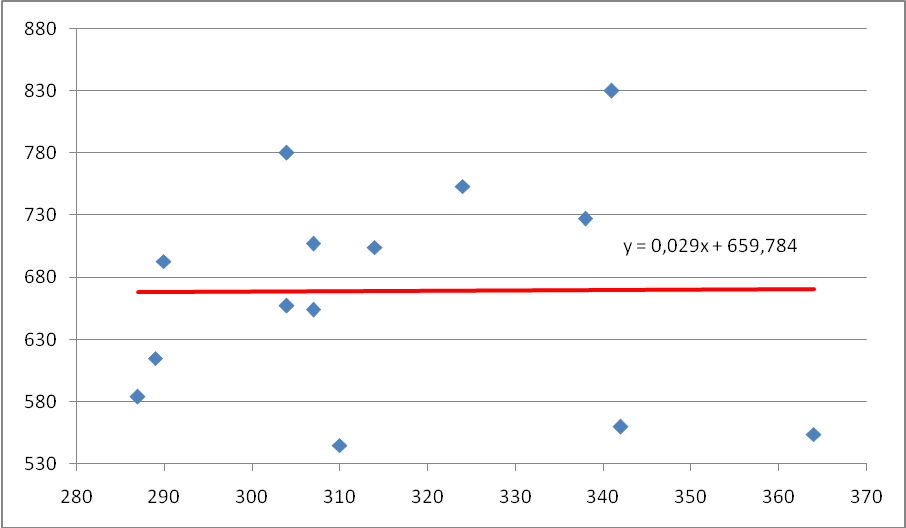
Рис.  1.2.   Линейная парная регрессия.

б)   Степенная парная регрессия рассчитывается по формуле:   ŷ = a∙ x^b .

Для определения параметров aи  bнеобходимо линеаризировать его, для чего логарифмируем его правую и левую части:  lg ŷ = lg a + b∙lg x.

Обозначим через ŷ* = lg ŷ,  a*= lg a,  x* = lg x. 

Тогда :  ŷ* = a* + b∙x*.

Используя значения, полученные в таблице 2, рассчитаем значения a и b:

b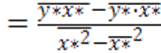 = (7,0496 – 2,8217∙ 2,4983)/(6,2426 – 2,4983∙2,4983) =

= -0,017.

a*  =  = 2,8217 – (- 0,017) ∙ 2,4983 =  2,864.

a =  =  = 731,814

Таким образом уравнение степенной регрессии будет иметь вид:

ŷ = 731,814 x^-0,017.

 

                                                                                              Таблица 3

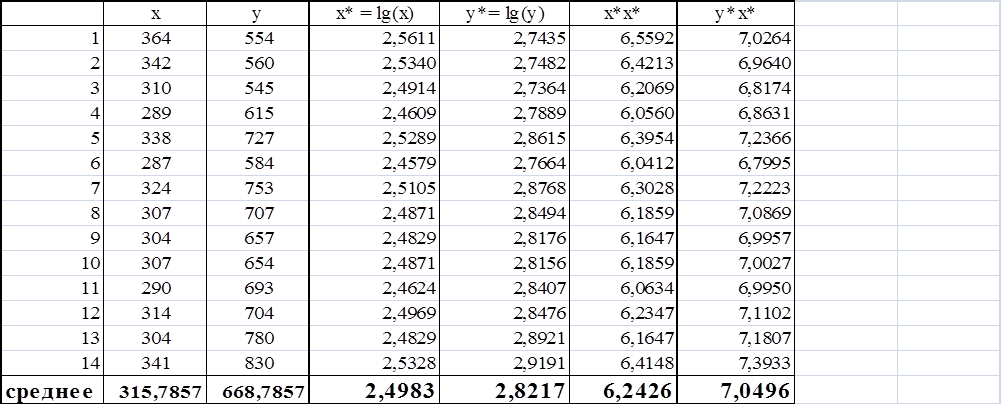
График степенной зависимости отражен на рис.1.3.:

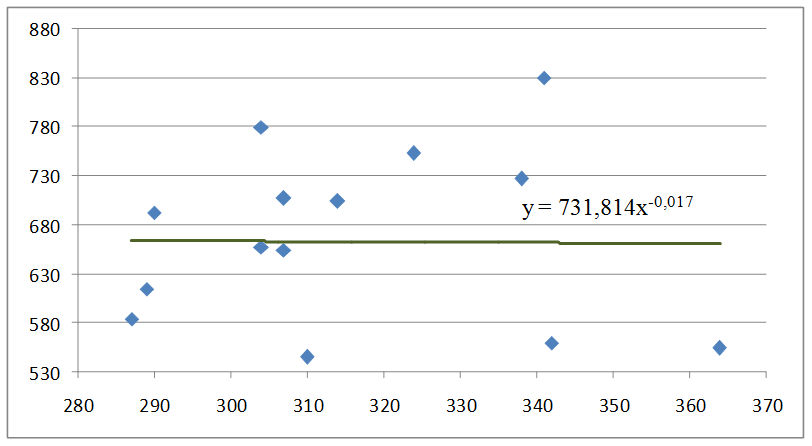
Рис.1.3. Степенная парная регрессия.

в)  Уравнение логарифмической регрессии представлено следующим уравнением:

ŷ = a + b∙lgx .

 Для определения параметров a и  b обозначим  lgx = x*, и представим уравнение логарифмической регрессии в виде  ŷ = a +b ∙x*.

          Используя значения, полученные в таблице 3, рассчитаем значения a и b:

b = 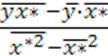 = (1670,9190 – 668,7857 ∙2,4983)/(6,2426 – 2,2483²) = 68,094.

a =  = 668,7857 – 68,094 ∙ 2,4983 = 498,6634.

Уравнение логарифмической регрессии будет иметь вид:

ŷ = 498,663  + 68,094∙lgx.

                                                                                                            Таблица 4

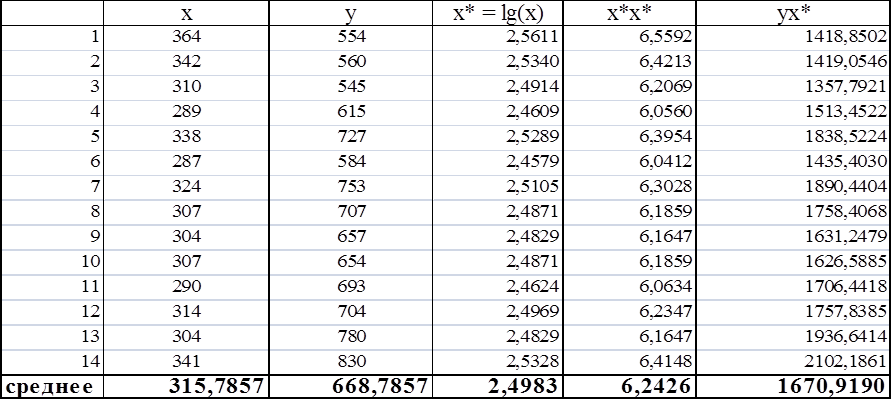
График логарифмической регрессии отражен на рис.1.4.

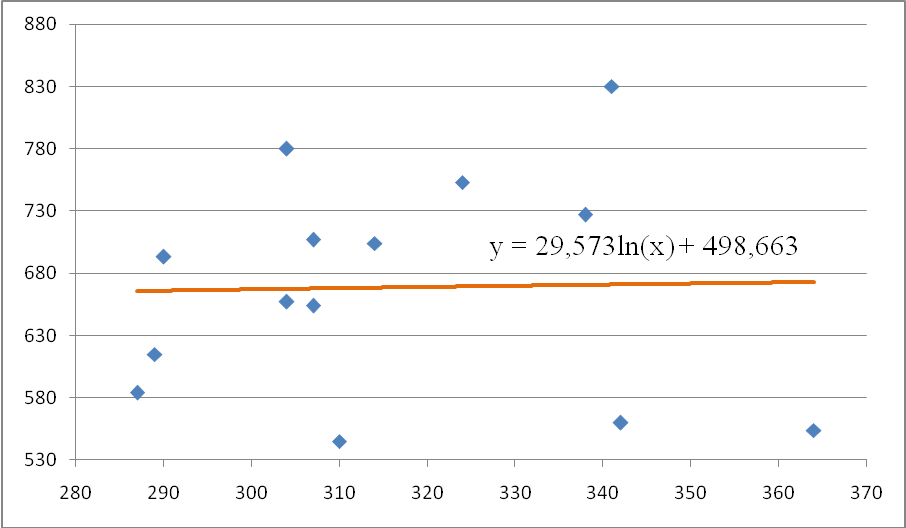
Рис. 1.4. Логарифмическая парная регрессии.

г)  Уравнение показательной регрессии имеет вид: ŷ = a ∙ b^x. Для определения параметров  a  и  b необходимо линеаризировать уравнение, для чего прологарифмируем правую и левую части уравнения:

lg ŷ =lg (a ∙ b^x) =lg a + x∙lg b .

Обозначим  lg ŷ = y*; lg a = a*; lg b = b*,  тогда  ŷ* = a* + b^* ∙x.