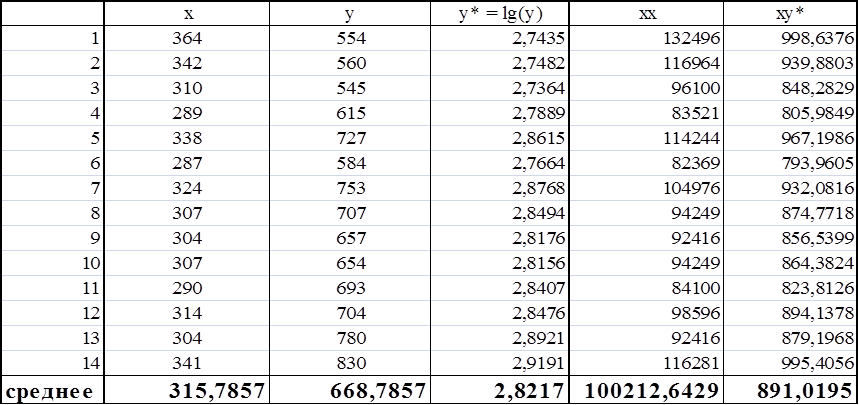
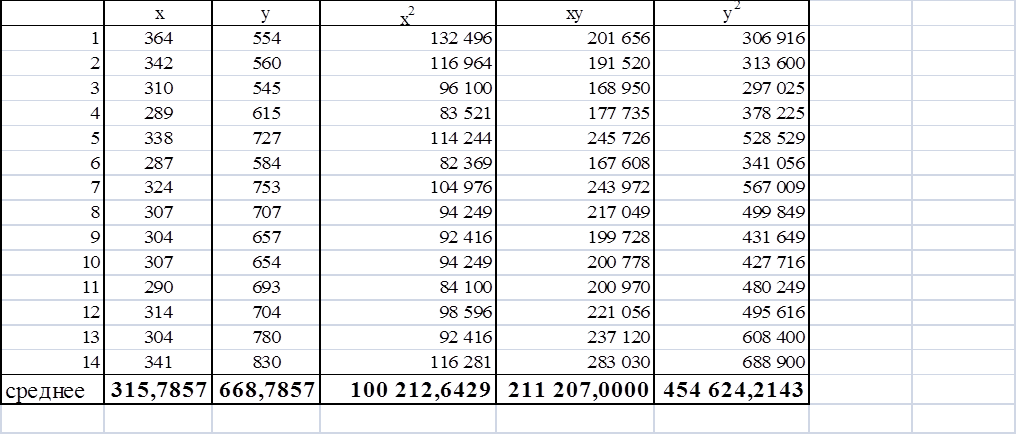
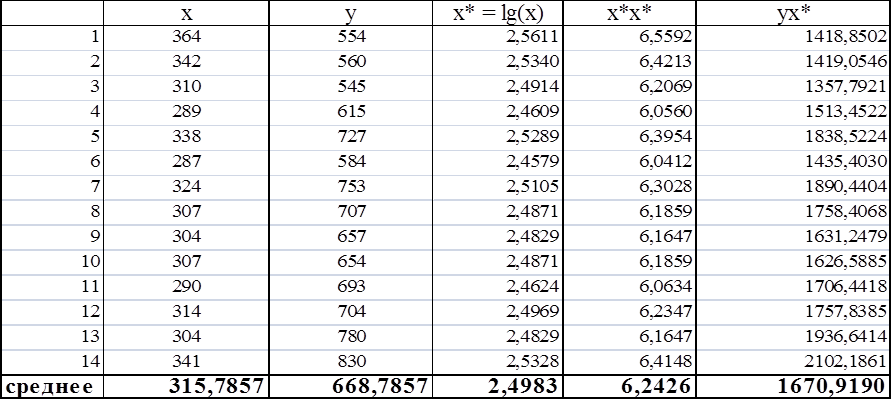
Используя данные таблицы 4, найдем значения параметров a* и b* :
Таблица 5
b* = 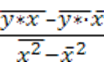 = (891,0195
– 2,8217 ∙ 315,7857)/(100212,6429 - 315,78572) =
= (891,0195
– 2,8217 ∙ 315,7857)/(100212,6429 - 315,78572) =
- 0,0001; b = 10b* = 10-0,0001 = 1,0.
a* = ![]() = 2,8217 – ( - 0,000065) ∙ 315,7857 = 2,8422
= 2,8217 – ( - 0,000065) ∙ 315,7857 = 2,8422
a = 10a* = 102.8422 = 695,37
Таким образом уравнение показательной регрессии будет иметь вид:
ŷ = 695,37 ∙ 1x.
График показательной зависимости отражен на рис.1.5.:
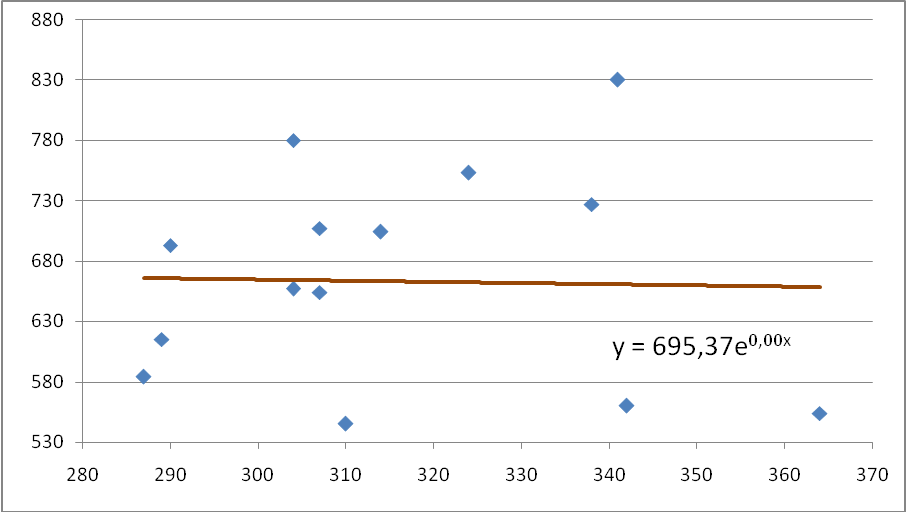
Рис. 1.5. Показательная парная регрессия.
3) Оценить тесноту связи с помощью показателей корреляции и детерминации.
а) коэффициент корреляции для линейной регрессии определяется по формуле:
 , где
, где ![]() ;
; 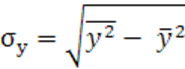 .
.
![]() =
= ![]() 22,1816
22,1816
![]() =
= ![]() = 85,7315
= 85,7315
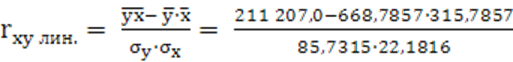 =
= 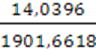 =
0,007
=
0,007
Таблица 6
 б)
коэффициент корреляции для логарифмической регрессии определяется по формуле:
б)
коэффициент корреляции для логарифмической регрессии определяется по формуле:
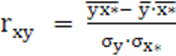
Таблица 7
![]() =
= ![]() 0,03
0,03
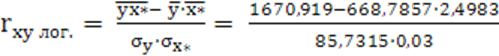 =
= 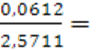 0,0238
0,0238
г) для степенной регрессии определяется индекс корреляции по формуле:
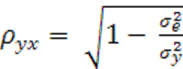 , где
, где
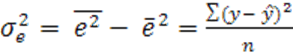 .
.
![]() =
0,0031 – 0,00022 = 0,0031
=
0,0031 – 0,00022 = 0,0031
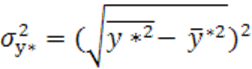 = 7,9651 – 2,82172 = 0,00313
= 7,9651 – 2,82172 = 0,00313
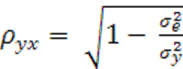 =
= 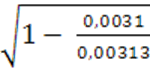 = 0,009
= 0,009
Таблица 8
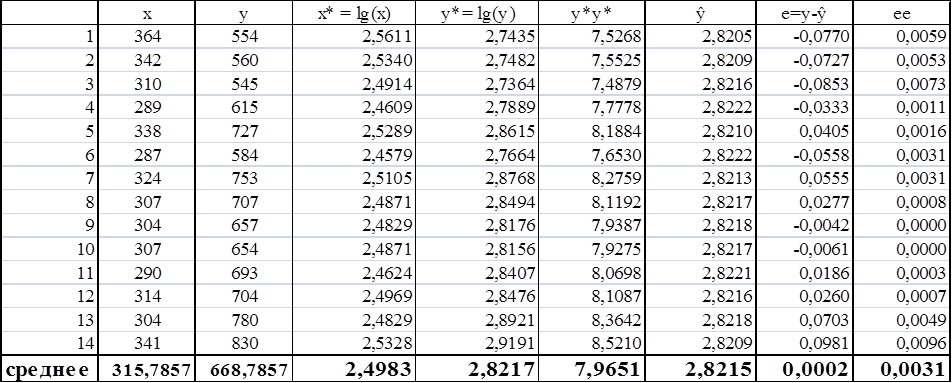
д) для показательной регрессии определяется индекс корреляции по формуле:
 , где
, где
 .
.
Таблица 9
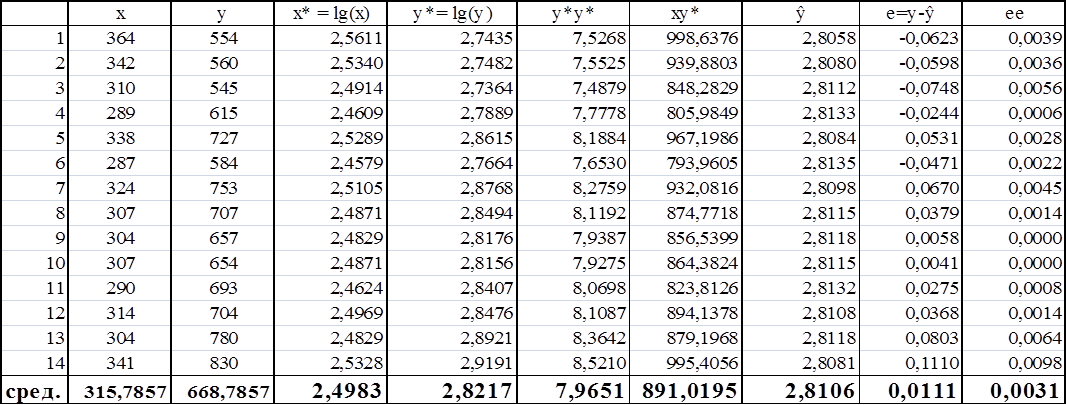
![]() =
0,0031 – 0,01112 = 0,003
=
0,0031 – 0,01112 = 0,003
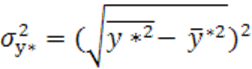 = 7,9651 – 2,82172 = 0,0031
= 7,9651 – 2,82172 = 0,0031
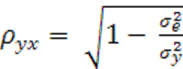 =
= 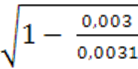 = 0,18
= 0,18
Исходя из значений коэффициентов корреляции для линейной и логарифмической регрессий, и индексов корреляции для показательной и степенной регрессий можно сделать вывод об отсутствии функциональной связи в линейной, логарифмической и степенной регрессиях, и о наличии слабой функциональной связи в показательной регрессии.
Коэффициент детерминации определяется по формуле:
а)
R2 = ![]() 2
= 0,0072 = 0,000049 -
коэффициент детерминации для линейной регрессии.
2
= 0,0072 = 0,000049 -
коэффициент детерминации для линейной регрессии.
б)
R2 = ![]() 2 = 0,02382 = 0,00057 - коэффициент
детерминации для логарифмической регрессии.
2 = 0,02382 = 0,00057 - коэффициент
детерминации для логарифмической регрессии.
в)
R2 = ![]() 2 = 0,0092 = 0,000081 - коэффициент
детерминации для степенной регрессии.
2 = 0,0092 = 0,000081 - коэффициент
детерминации для степенной регрессии.
г)
R2 = ![]() 2 = 0,182
= 0,0324 - коэффициент детерминации для показательной регрессии.
2 = 0,182
= 0,0324 - коэффициент детерминации для показательной регрессии.
Наибольший коэффициент детерминации вычислен для показательной регрессии - 0,0324, следовательно из всех представленных уравнений уравнение показательной регрессии объяснит 3% дисперсии результативного фактора.
4) Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в п.3 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.
Определим значение фактического Fфакт. :
а) для линейной регрессии:
Fфакт. = 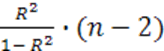 =
= 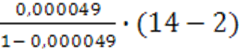 =
0,000059
=
0,000059
б) для логарифмической регрессии:
Fфакт. = 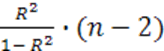 =
= 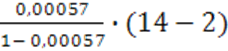 =
0,0068
=
0,0068
в) для степенной регрессии:
Fфакт. = 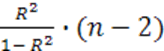 =
= 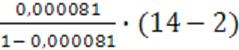 =
0,00097
=
0,00097
г) для показательной регрессии:
Fфакт. = 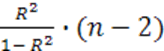 =
= 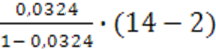 =
0,4018
=
0,4018
Fтабл. при уровне значимости α = 0,05, при одной независимой переменной равен 4,75. Из полученных показателей ни один не превышает табличного значения F-критерия Фишера, значит вероятность нулевой гипотезы выше заданного уровня. Отсюда можно сделать вывод, что ни одно из уравнений не является статистически значимым, т.е. признается ненадежность уравнений регрессий.
5) Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7 % от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Расчет для сравнения:
- для линейной регрессии:
х0=![]() *1,07= 315,7857 * 1,07 = 337,891.
*1,07= 315,7857 * 1,07 = 337,891.
ŷx0 = a + b ∙ x = 659,7840 + 0,029 ∙ 337,891 = 669,583
tа=2,179.
![]() =
= 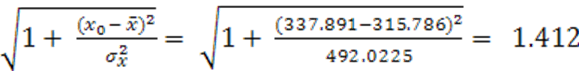
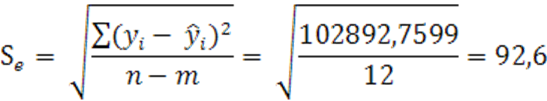
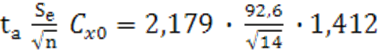 =
55,34
=
55,34
Интервал 669,583 – 55,34![]() 669,583
+ 55,34, т.е
669,583
+ 55,34, т.е
614,246![]() 724,923.
724,923.
- для степенной регрессии:
х0=![]() *1,07= 315,7857 * 1,07 = 337,891
*1,07= 315,7857 * 1,07 = 337,891
![]() 662,842
662,842
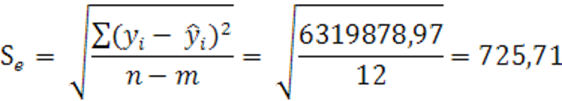
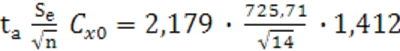 = 596,69
= 596,69
Интервал 669,583 – 596,69![]() 669,583
+ 596,69, т.е
669,583
+ 596,69, т.е
72,89![]() 1266,28.
1266,28.
- для показательной регрессии:
х0=![]() *1,07= 315,7857 * 1,07 = 337,891.
*1,07= 315,7857 * 1,07 = 337,891.
![]() 695,37*1,0337,891= 695,37
695,37*1,0337,891= 695,37
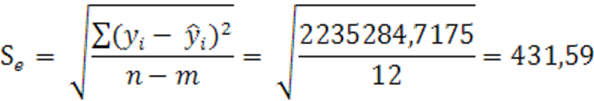
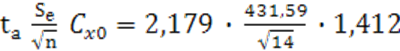 = 354,86
= 354,86
Интервал 669,583 – 354,86 ![]() 669,583
+ 354,84, т.е
669,583
+ 354,84, т.е
314,72![]() 1024,42.
1024,42.
- для логарифмической регрессии:
х0=![]() *1,07= 315,7857 * 1,07 = 337,891.
*1,07= 315,7857 * 1,07 = 337,891.
![]() 498,663
+ 68,094 ∙ lg 337,891 = 670,86
498,663
+ 68,094 ∙ lg 337,891 = 670,86
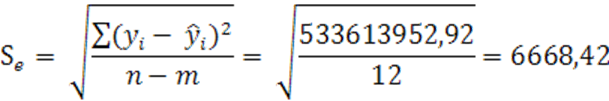
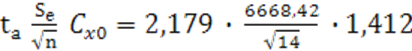 = 2966,66
= 2966,66
Интервал 669,583 – 6668,42 ![]() 669,583
+ 6668,42, т.е
669,583
+ 6668,42, т.е
-5998,84![]() 7333,0.
7333,0.
Список использованных источников.
1. Эконометрика: Учебное пособие. – Комсомольск-на-Амуре: ГОУВПО «КнАГТУ», 2005 – 138 с.
2. Эконометрика: Учебник / Под ре. И.И. Елисеевой. – М.; Финансы и статистика, 2002. – 344с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.