Действия над событиями. Классическое и статистическое определения вероятности.

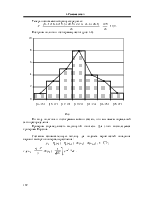
4. РЕШЕНИе ЗАДАЧ

4.1. Задачи к главе 1

4.1.1. Действия над событиями

Пример 4.1. Что означают события  ?

Ответ. Событие означает наступление обоих событий A и B.

Событие  означает один из трех вариантов:

а) наступление события A, б) наступление события B, в) наступление и события A, и события B.

Пример 4.2.  Пусть события A₁ , A₂ , A₃  – климатические  факторы, снижающие урожайность: A₁ – поздняя весна; A₂ – летняя засуха; A₃ – дождливая осень;  – наилучшие климатические условия для созревания урожая. Найти выражения для событий: а) A – ни одного фактора, снижающего урожай; б) B – только один фактор; в) С – только два фактора; г) D – три фактора, снижающих урожай; д) E – хотя бы один фактор; е) F – хотя бы два фактора из трех.

Ответ. а) ; б) , где произведения  – попарно несовместные события; в) , где произведения  – попарно несовместные события; г) ; д) ; е) .

4.1.2. Классическое и статистическое определения вероятности

Классическое определение вероятности

Вероятность события A принято обозначать символом P(A) (от слова probabilitas – вероятность).

По классическому определению вероятностью события P(A) называется величина, определяемая по формуле (1.5):

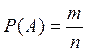, где m – число исходов опыта, благоприятствующих событию A, n – общее число всех несовместных равновозможных элементарных исходов.

Статистическое определение вероятности

Относительной частотой W(A) события A называется величина, определяемая по формуле

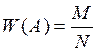, где М – число испытаний, в которых событие произошло, N– общее число испытаний.

Установлено, что относительная частота обладает свойством устойчивости, состоящим в том, что в различных опытах, проводимых при неизменных условиях, W(A) изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа, равного численному значению вероятности P(A).

Пример 4.3. Лотерейные билеты выпущены на общую сумму a руб. Цена одного билета b руб. Ценные выигрыши выпадают на k билетов. Определить вероятность ценного выигрыша на один билет.

Решение. Обозначим  событие A – выигрыш по лотерейному билету. Всего билетов  .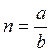

Число билетов, благоприятствующих наступлению события A, . Искомая вероятность будет равна:

.

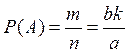Пример 4.4.  Монета подброшена пять раз. Герб выпал два раза. Какова вероятность и относительная частота выпадения герба?

Решение. Обозначим событие A – выпадение герба. Вероятность:

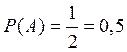, так как при подбрасывании монеты выпадению герба из двух равновозможных исходов n = 2 благоприятствует один m = 1.

Относительная частота выпадения герба равна:

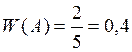, так как событие наступило два раза M = 2 в пяти испытаниях N = 5.

Примечание. При увеличении числа  подбрасываний монеты относительная частота W(A) будет приближаться к численному значению P(A).

4.1.3. Элементы комбинаторики в теории вероятностей

Комбинаторикой называется раздел математики, исследующий множества и правила составления комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три основных типа комбинаций: перестановки, размещения, сочетания.

n – факториалом называется произведение первых n натуральных чисел. Обозначается:

.

Перестановками называются комбинации, состоящие из n элементов, которые отличаются друг от друга порядком следования элементов.

Число перестановок обозначается  и вычисляется по формуле:

.

Размещениями называются комбинации, составленные из n различных элементов по m элементов в каждой комбинации, отличающиеся друг от друга или самими элементами, или порядком следования элементов в комбинации.

Число размещений обозначается  и вычисляется по формуле

.

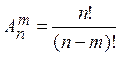Сочетаниями называются комбинации, составленные из n различных элементов по m элементов в каждой комбинации, отличающиеся друг от друга хотя бы одним элементом.

Число сочетаний обозначается  и вычисляется по формуле .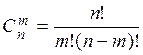

Пример 4.5. Вычислить .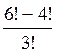

Решение.  .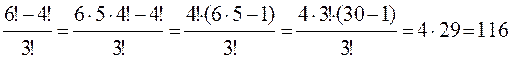

Пример 4.6. Упростить .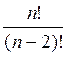

Решение. .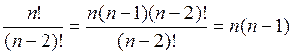

Пример 4.7. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, чтобы ни одна из них не повторилась?

Решение. Так как двузначные числа отличаются друг от друга или самими цифрами, или порядком их следования, то искомое количество двузначных чисел равно числу размещений  из пяти цифр n = 5 по две m = 2 в каждой комбинации:

.

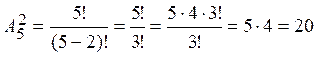Итак, можно составить 20 различных двузначных чисел из пяти цифр