Глава 2. Случайные величины
2.1. Определение и примеры случайных величин
Рассмотрим
вероятностное пространство (![]() ).
).
Однозначная числовая функция, заданная на пространстве элементарных исходов, называется случайной величиной.
Обозначения:
![]() , …
, …
Таким
образом, ![]() ,
, ![]() .
.
В соответствии с определением, случайная величина
каждому элементарному исходу из пространства ![]() , в
зависимости от случая, ставит в соответствие одно определенное числовое
значение.
, в
зависимости от случая, ставит в соответствие одно определенное числовое
значение.
Значения функции ![]() будем
называть возможными значениями случайной величины
будем
называть возможными значениями случайной величины ![]() .
.
Приведем несколько примеров случайных величин.
Пример 2.1. Эксперимент – подбрасывание игральной кости.
Пространство элементарных исходов: ![]() , где
, где
![]() – на грани игральной кости выпало
– на грани игральной кости выпало ![]() очков,
очков, ![]() .
.
Пусть
![]() – число очков, выпавших на грани игральной
кости.
– число очков, выпавших на грани игральной
кости.
Возможные
значения ![]() : 1, 2, ..., 6.
: 1, 2, ..., 6.
Пример
2.2. Эксперимент – последовательность из ![]() независимых
испытаний в схеме Бернулли.
независимых
испытаний в схеме Бернулли.
Пространство элементарных исходов:
![]() , где
, где
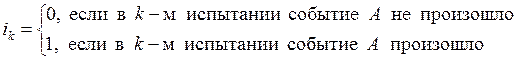 .
.
Пусть
![]() – число появлений события А в этих
испытаниях.
– число появлений события А в этих
испытаниях.
Возможные
значения ![]() : 0, 1, ...,
: 0, 1, ..., ![]() .
.
Пример 2.3. Эксперимент – регистрация вызовов в течение часа на АТС.
Пространство элементарных исходов – ![]() .
.
Пусть ![]() – число вызовов, поступивших на
АТС в течение часа.
– число вызовов, поступивших на
АТС в течение часа.
Возможные
значения ![]() : 0, 1, ...
: 0, 1, ...
Пример 2.4. Эксперимент – бросание случайной точки в квадрат со стороной 1.
Пространство элементарных исходов:
![]() , где
, где
![]() декартовы координаты точки на плоскости.
декартовы координаты точки на плоскости.
Пусть
![]() – расстояние от начала координат до точки
– расстояние от начала координат до точки ![]() .
.
Возможные
значения ![]() :
: ![]() .
.
Если пространство элементарных исходов, на котором задается случайная величина, конечное (примеры 2.1 – 2.2) или счётное (пример 2.3), то эта случайная величина называется дискретной (принимает отдельные изолированные значения).
Если пространство элементарных исходов бесконечное, несчётное и связное (пример 2.4), то случайная величина называется непрерывной (имеет несчетное множество значений).
2.2. Закон распределения дискретной случайной величины
Пусть пространство элементарных исходов ![]() - конечное или счётное множество. Во
втором случае будем считать, что n равно бесконечности.
- конечное или счётное множество. Во
втором случае будем считать, что n равно бесконечности.
Наибольший интерес представляют вероятности, с которыми случайная величина принимает каждое из своих возможных значений.
Обозначим через ![]() событие,
которое заключается в том, что m принимает своё i-е
значение,
событие,
которое заключается в том, что m принимает своё i-е
значение, ![]() . Появление события
. Появление события ![]() означает,
что в результате эксперимента имел место элементарный исход
означает,
что в результате эксперимента имел место элементарный исход ![]() , поэтому
, поэтому
![]() .
.
Множество пар чисел ![]() называется
законом распределения дискретной случайной величины.
называется
законом распределения дискретной случайной величины.
Закон распределения обычно представляется в виде таблицы, состоящей из двух строк, в первой из которых записываются возможные значения случайной величины, а во второй – вероятности, с которыми эти возможные значения принимаются
|
|
|
|
… |
|
|
|
|
|
… |
|
При
этом 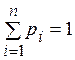 так как по определению
так как по определению 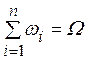 и
и
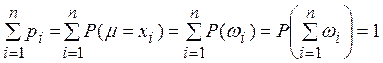
(![]() –
несовместные события).
–
несовместные события).
2.2.1. Основные дискретные распределения
Равномерное
распределение на множестве ![]()
Возможные
значения: ![]()
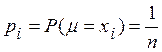 .
.
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Биномиальное распределение
В последовательности из n независимых испытаний
схемы Бернулли, ![]() – число появлений события А
в этих испытаниях.
– число появлений события А
в этих испытаниях.
Возможные
значения ![]() :
: ![]() ;
;
![]() .
.
|
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
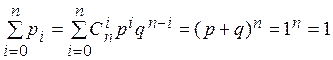 .
.
Распределение Пуассона
Рассмотрим последовательность независимых испытаний
при ![]() , случайная величина
, случайная величина ![]() – число появлений события
– число появлений события ![]() в этих испытаниях.
в этих испытаниях.
Возможные значения: 0, 1, 2, …; 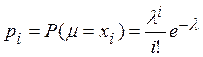 .
.
|
|
|
|
… |
|
… |
P |
|
|
… |
|
… |
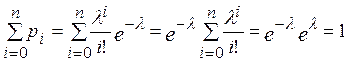 .
.
Здесь использовано известное разложение показательной функции в ряд Маклорена
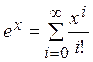 .
.
Геометрическое распределение
Рассмотрим последовательность независимых испытаний.
Случайная величина ![]() – число испытаний, проведённых
до первого появления события А.
– число испытаний, проведённых
до первого появления события А.
Возможные значения: 1, 2, 3, …;
![]() .
.
|
|
1 |
2 |
… |
|
… |
|
|
|
|
… |
|
… |
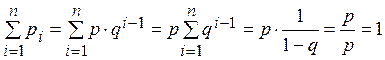 .
.
Гипергеометрическое распределение
Имеется ![]() объектов произвольной
природы. Среди них
объектов произвольной
природы. Среди них ![]() объектов обладают некоторым
свойством
объектов обладают некоторым
свойством ![]() . Наудачу отбираются
. Наудачу отбираются ![]() объектов. Случайная величина
объектов. Случайная величина ![]() – число объектов среди отобранных,
обладающих свойством
– число объектов среди отобранных,
обладающих свойством ![]() .
.
Возможные значения: ![]() , где
, где
![]() ,
, ![]() ; при
этом
; при
этом 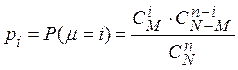 .
.
2.3. Функция распределения случайной величины
Функция ![]() , равная вероятности того,
что случайная величина
, равная вероятности того,
что случайная величина ![]() примет значение меньшее
примет значение меньшее ![]() , называется функцией распределения этой
случайной величины
, называется функцией распределения этой
случайной величины ![]() , т. е.
, т. е.
![]() . (2.1)
. (2.1)
Геометрически, функция распределения – это вероятность
того, что случайная величина примет значение, которое расположено на числовой
оси левее точки ![]() .
.
Пусть ![]() дискретная случайная
величина, заданная законом распределения.
дискретная случайная
величина, заданная законом распределения.
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Построим функцию распределения этой случайной величины.
Для
удобства предположим, что ![]() , тогда
, тогда
1)
Если ![]() , то
, то ![]() .
.
2)
Если ![]() , то
, то ![]() .
.
3)
Если ![]() , то
, то ![]()
![]() .
.
4)
Если рассматривается k-й промежуток ![]() , то
, то
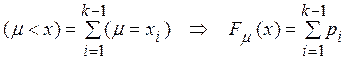 .
.
5) Если ![]() , то
, то ![]() .
.
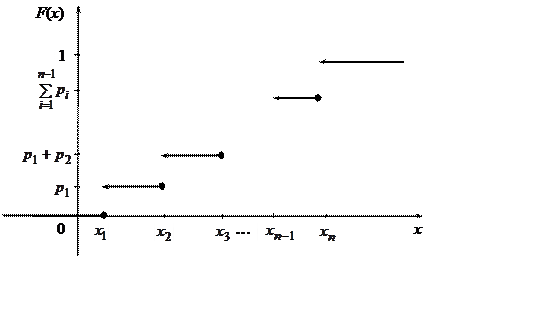 |
Рис. 2.1
Для любой дискретной случайной величины функция распределения есть кусочно-постоянная функция.
Случайная величина ![]() называется
непрерывной, если её функция распределения непрерывна.
называется
непрерывной, если её функция распределения непрерывна.
Основные свойства функции распределения:
10. Функция распределения ограничена ![]() , так как функция распределения – это
вероятность появления некоторого случайного события
, так как функция распределения – это
вероятность появления некоторого случайного события
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.