Купонная ставка по облигации, со сроком погашения 1 год составляет 50%. Номинальная стоимость облигации 1 тыс. руб., рыночная 1,1 тыс. руб. Какова цена сделки-продажи данной облигации?
Ответ:
Цена сделки-продажи данной облигации 1,1 тыс. руб.
Задача 3.
Инвестор А купил акции по цене 500 руб., а через месяц продал их с прибылью инвестору В, который спустя месяц покупки также перепродал эти акции инвестору С, но по цене равной 1000 руб. Определите, по какой цене инвестор В купил акции у инвестора А, если известно, что оба инвестора получили одинаковую доходность (дивиденды при этом не выплачивались)?
Решение:
Доходность (норма отдачи) акции определяется по формуле:
r = (Рк – Рн )/ Рн , где Рк - цена продажи акции (конечная цена),
Рн - цена покупки акции (начальная цена).
RА = (РкА – РнА )/ РнА *100
RВ = (РкВ – РнВ )/ РнВ *100
РкА = РнВ = Х
Из условия задачи известно, что доходность инвестора А и доходность инвестора В равны:
RА = RВ = > (Х– РнА )/ РнА = (РкВ – Х)/ Х
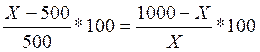
(X-500)*X= (1000-X)*500
X2-500X= 500000-500X
X2=500000
X=707
Проверка:
RА = ((РкА – РнА )/ РнА ) *100 =(707-500) / 500 * 100 = 41,44
RВ = ((РкВ – РнВ )/ РнВ) * 100 = (1000-707)/707 * 100 = 41,44
Ответ:
Инвестор В купил акции у инвестора А по цене 707 рублей.
Задача 4.
Инвестор приобрел привилегированную акцию (номинальной стоимостью 250 руб.) по цене 300руб., с фиксированным дивидендом -20% годовых. Через два года инвестор продал акцию за 280 руб. Определите конечную доходность акции (в пересчете на год), если известно, что в течение этих двух лет дивиденды выплачивались полностью.
Решение:
Доходность (норма отдачи) акции за холдинговый период определяется по формуле:
r = (Рк – Рн + D)/ Рн , где Рк - цена продажи акции (конечная цена),
Рн - цена покупки акции (начальная цена).
D – денежные суммы, начисленные по ценной бумаге за холдинговый период.
Определим норму отдачи ц/б за холдинговый период по формуле (3.3)
r =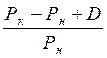 =
= 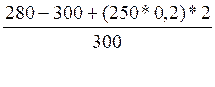 *100 = 26,67%
*100 = 26,67%
Ответ: Конечная доходность акции 26,67%
Задача 5.
Облигация с купоном, равным 10% имеет рыночную стоимость 95%. Определить текущую доходность облигации
Решение:
Определим текущую доходность облигации Дто по формуле (3.12)
Дто = К/Р, где К – ставка купона,
Р – курсовая цена облигации с учетом накопленного купонного дохода.
Дто = 10/95*100 = 10,5%
Ответ: Текущая доходность облигации 10,5%.
Задача 6.
Номинальная стоимость акции составляет 1000 руб., ожидаемый размер дивиденда - 40%. Определите ориентировочную курсовую стоимость акции, если ставка банковского процента составляет 30%.
Решение:
Доход по акции определяется из формулы:
Р = D/R * 100, где D – доход по акции, равный дивиденду и изменению курсовой стоимости;
Р – расчетная цена акции, равная сегодняшней стоимости будущих доходов по ней;
R – текущая рыночная ставка процента на срок, за который выплачивается дивиденд.
Определим доход по акции:
D= P*R / 100 = (1000*40)/100= 400 руб.
Определим расчетную цену акции R = D/ P *100=(1000*30)/100=300 руб.
Курсовая стоимость акции равна Р = D/R *100 ; Р= 400/300*100=133,33%
1,33*1000=1330 руб.
Задача 7.
Номинал банковской акции составляет 1000 руб., текущая рыночная цена -2800руб. Банк выплачивает квартальный дивиденд в размере 200 руб. на одну акцию. Определите текущую годовую доходность акции.
Решение:
Текущая доходность акции определяется по формуле:
r = D / P * 100;
где D - дивиденд по акции,
Р – курсовая цена акции
r = 200 * 4 / 2800 *100 = 28,57%
Ответ: текущая годовая доходность акции 28,57%.
Задача 8.
Инвестор приобрел две облигации номиналом в 1000 руб. каждая. Доход по одной из них составляет -10%, по другой- 8,5%. Определите разность годового дохода по этим облигациям.
Решение:
Определим годовой доход по первой облигации
Д = 1000*10%=100 руб.
Определим годовой доход по второй облигации
Д = 1000*8,5% =85 руб.
Разность по облигациям равна
100-85=15 руб.
Ответ: разность годового дохода по облигациям равна 15 руб.
Задача 9.
Инвестор приобрел государственную бескупонную облигацию на вторичных торгах по цене, равной 91,12% к номиналу, за 20 дней до ее погашения. Рассчитайте доходность ГКО к моменту ее погашения с учетом налоговых льгот.
Решение:
Доходность к моменту погашения с учетом налоговых льгот рассчитаем по формуле:
Yп =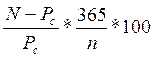 ;
;
Yп = 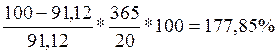
Ответ: Доходность к моменту погашения с учетом налоговых льгот составит 177,85%.
Задача 10.
Определите накопленный купонный доход по облигации федерального займа с переменным купоном и номиналом 1 млн. руб., с текущим купонным периодом 92 дня и купонной ставкой, равной 50% , если она приобретена за 10 дней до ближайшей выплаты.
Решение:
Определим величину купона по формуле:
С =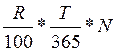 ; где R –купонная ставка (в процентах годовых);
; где R –купонная ставка (в процентах годовых);
Т – текущий купонный период (в календарных днях).
С = 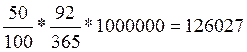 руб.
руб.
Определим накопленный купонный доход по формуле (3.30)
А=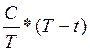
А = 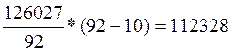 руб.
руб.
Ответ: накопленный купонный доход по ОФЗ 112328 руб.
Задача 11.
Инвестор приобрел облигацию государственного внутреннего валютного займа по цене 50% от номинала и продал ее спустя 72 дня за 54% от номинала. Определите совокупный доход инвестора от этой операции (без учета налогообложения).
Решение:
Совокупный доход по данной операции будет складываться:
- из разницы между ценами продажи и покупки, и из накопленного купонного дохода.
Доход от операции без учета накопленного дохода составит:
54% - 50% = 4%
Величину купона определим по формуле:
С = R/100 * T/365 *N,
Где R – купонная ставка (для облигаций государственного внутреннего валютного займа R=3% годовых),
Т – текущий купонный период в календарных днях,
N – номинал облигации.
С = 3/100 * 72/365 * 100 = 0,59%
Совокупный доход от операции составит:
4% + 0,59% = 4,59%
Ответ: совокупный доход инвестора от этой операции 4,59%.
Задача 12.
Облигация номиналом 1000 руб. выпущена на срок, равный одному году с купоном -30 %, и размещена с дисконтом равным -10%. Во сколько раз ее конечная доходность будет выше ее текущей доходности?
Решение:
1. Текущая доходность облигации определяется по формуле:
Д то = К/Р * 100;
где К – ставка купона (30%);
Р – курсовая цена облигации
Р = 1000-1000*10% =900 руб.
Д то = 1000*30%/900 * 100 = 33,3%
2. Конечная доходность облигации определяется по формуле:
Дко = (К +N - P) / (Р*n), где К –величина купона,
N – цена погашения облигации,
Р – курсовая цена облигации,
n – количество лет до погашения.
Дко = (1000*30% + 1000 -900) / (900*1) = 0,44 = 44,4%
3. Определим, во сколько раз конечная доходность будет выше текущей:
Дко / Д то = 44,4 / 33,3 = 1,33
Ответ: конечная доходность облигации будет выше текущей в 1,33 раза
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.