Определение.
Пусть дана бесконечная числовая последовательность ![]()
![]() Выражение вида:
Выражение вида:
![]() (2.1)
(2.1)
называется числовым рядом.
Числа ![]() называются членами ряда
(2.1), член an
называют общим членом ряда (
называются членами ряда
(2.1), член an
называют общим членом ряда (![]() ).
).
Сокращённое обозначение ряда
(2.1): 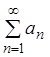 .
.
Определение.
Сумма n первых членов ряда называется n-й частичной суммой рядаи обозначается: ![]() , т.е.
, т.е. ![]() .
.
Рассмотрим последовательность частичных сумм:
![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() , …
, …
Определение.
Если существует конечный предел ![]() последовательности
частичных сумм
последовательности
частичных сумм ![]() :
: ![]() , то
ряд (2.1) называют сходящимся, а число S называют суммой
ряда (2.1). В этом случае пишут:
, то
ряд (2.1) называют сходящимся, а число S называют суммой
ряда (2.1). В этом случае пишут: 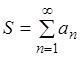 . Если
последовательность
. Если
последовательность ![]() не имеет конечного предела, то
ряд (2.1) называют расходящимся.
не имеет конечного предела, то
ряд (2.1) называют расходящимся.
Пример 1. Доказать, что ряд
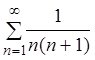 сходится.
сходится.
Решение. Возьмём сумму ![]() первых n членов ряда:
первых n членов ряда:
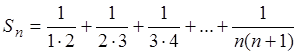 .
.
Слагаемые этой суммы могут быть представлены в виде:
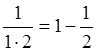 ,
, 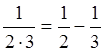 ,
, 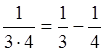 , …,
, …, 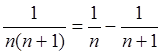 .
.
Поэтому
 .
.
Отсюда следует, что предел последовательности частичных
сумм данного ряда равен единице: 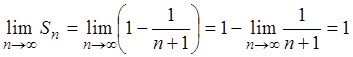 .
.
Таким образом,
ряд  сходится и его сумма S = 1.
сходится и его сумма S = 1.
Пример 2. Исследовать ряд на сходимость:
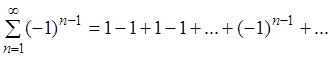
Решение.
Последовательность частичных сумм ряда имеет вид: ![]()
![]()
![]()
![]() ,
,
![]() … и, значит, не сходится ни к какому
пределу, поэтому данный ряд расходится.
… и, значит, не сходится ни к какому
пределу, поэтому данный ряд расходится.
Пример 3. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии (а – первый член геометрической прогрессии, q – знаменатель прогрессии):
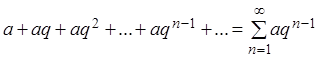 . (2.2)
. (2.2)
Решение. Частичная
сумма ![]() этого ряда при
этого ряда при ![]() имеет вид:
имеет вид:
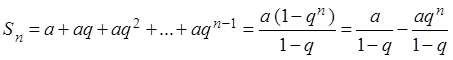 , здесь использована формула суммы первых
, здесь использована формула суммы первых ![]() членов геометрической прогрессии.
членов геометрической прогрессии.
Отсюда:
1)
если ![]() , то
, то  , т.е.
ряд сходится и его сумма:
, т.е.
ряд сходится и его сумма: 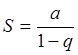 . Например, при а =
1,
. Например, при а =
1, 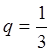 имеем:
имеем:
 ;
;
2)
если ![]() , то
, то
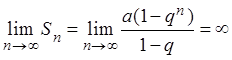 , т.е. ряд расходится;
, т.е. ряд расходится;
3)
|
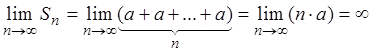 ,
т.е. ряд расходится;
,
т.е. ряд расходится;
4)
при ![]() ряд (2.2) принимает вид:
ряд (2.2) принимает вид: ![]() Его частичные суммы
Его частичные суммы ![]() при n
чётном и
при n
чётном и ![]() при n
нечётном. Следовательно,
при n
нечётном. Следовательно, ![]() не существует и ряд
расходится. Таким образом, ряд (2.2) является сходящимся при
не существует и ряд
расходится. Таким образом, ряд (2.2) является сходящимся при ![]() и расходящимся при
и расходящимся при ![]() .
.
Определение. Если в выражении (2.1) отбросить n первых членов, то оставшийся ряд
![]()
называют n-м остатком ряда
(2.1) и обозначают ![]() .
.
Если (2.1) сходится, то ![]() .
.
Сходимость или расходимость числового ряда не нарушается, если в нём отбросить любое конечное число членов. Но его сумма, если она существует, при этом изменяется.
Свойства сходящихся рядов:
1)
если ряд 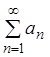 сходится и его сумма равна S, то и ряд
сходится и его сумма равна S, то и ряд 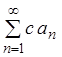 , где с – некоторое
действительное число, также сходится, и его сумма равна
, где с – некоторое
действительное число, также сходится, и его сумма равна ![]() ;
;
2)
если ряды 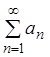 и
и ![]() сходятся
и их суммы соответственно равны SI и SII, то и ряд
сходятся
и их суммы соответственно равны SI и SII, то и ряд 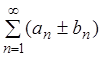 сходится и его сумма
равна: SI ± SII.
сходится и его сумма
равна: SI ± SII.
В приложениях применяются только сходящиеся ряды, поэтому по данному ряду необходимо, прежде всего, определить, является ли он сходящимся. Исследование сходимости рядов проводится с помощью теорем, называемых признаками сходимости.
Теорема 2.1 (необходимый
признак сходимости ряда). Если числовой ряд 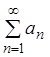 сходится,
то
сходится,
то ![]() .
.
Доказательство.
Пусть ряд 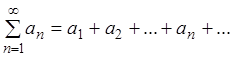 сходится, т.е. имеет место
равенство:
сходится, т.е. имеет место
равенство: ![]() , где S –
сумма ряда; но тогда имеет место также равенство
, где S –
сумма ряда; но тогда имеет место также равенство ![]() . Вычитая
почленно из первого равенства второе, получаем:
. Вычитая
почленно из первого равенства второе, получаем:
![]() ,
, ![]() .
.
Но ![]() .
Следовательно,
.
Следовательно, ![]() , что и требовалось доказать.
, что и требовалось доказать.
Заметим, что
этот признак сходимости не является достаточным. Если ![]() ,
то ряд может быть сходящимся или может быть расходящимся. Так, для ряда
,
то ряд может быть сходящимся или может быть расходящимся. Так, для ряда 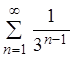 из примера 3 предел общего члена ряда
равен:
из примера 3 предел общего члена ряда
равен: 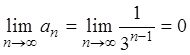 , и этот ряд сходится.
, и этот ряд сходится.
Определение. Ряд
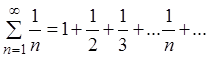 (2.3)
(2.3)
называется гармоническим рядом.
Гармонический
ряд (2.3) является расходящимся (как будет показано в разд. 2.2,
пример 5), хотя  . Таким образом, если
. Таким образом, если ![]() (т.е. если общий член ряда стремится к
нулю), то ещё нельзя сделать вывод о сходимости ряда. Необходимо дополнительное
исследование, которое может быть проведено с помощью достаточных условий
(признаков) сходимости ряда. Кроме того, из теоремы 2.1 можно сделать вывод о
достаточном признаке расходимости ряда.
(т.е. если общий член ряда стремится к
нулю), то ещё нельзя сделать вывод о сходимости ряда. Необходимо дополнительное
исследование, которое может быть проведено с помощью достаточных условий
(признаков) сходимости ряда. Кроме того, из теоремы 2.1 можно сделать вывод о
достаточном признаке расходимости ряда.
Теорема
2.2 (достаточный признак расходимости ряда).Если ![]() , то ряд
, то ряд 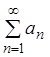 расходится.
расходится.
Пример 4. Исследовать на сходимость ряд: 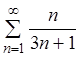 .
.
Решение. Запишем общий член данного ряда 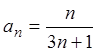 .
Тогда
.
Тогда
 , т.е. ряд расходится.
, т.е. ряд расходится.
Теорема 2.3 (признак сравнения). Пусть даны два ряда с положительными членами
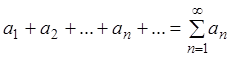 ,
(*)
,
(*)
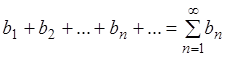 ,
(**)
,
(**)
и для всех ![]() выполняются неравенства
выполняются неравенства
![]() ,
(***)
,
(***)
тогда: 1) из сходимости ряда (**) следует сходимость ряда (*);
2) из расходимости ряда (*) следует расходимость ряда (**).
Доказательство
1) Обозначим
через ![]() и
и ![]() соответственно
частичную сумму первого и второго рядов, т.е.
соответственно
частичную сумму первого и второго рядов, т.е. 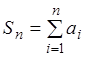 ,
, 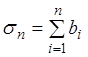 . Из условия (2.6) следует, что
. Из условия (2.6) следует, что ![]() . Так как ряд (**) сходится, то существует
предел
. Так как ряд (**) сходится, то существует
предел ![]() его частичных сумм:
его частичных сумм:
![]() .
.
Из того, что
члены рядов (*) и (**) положительны, следует, что ![]() , и тогда
в силу неравенства
, и тогда
в силу неравенства ![]() получаем:
получаем: ![]() . Таким образом, мы доказали, что частичные
суммы
. Таким образом, мы доказали, что частичные
суммы ![]() ограниченны. Кроме того, при увеличении
ограниченны. Кроме того, при увеличении ![]() частичная сумма
частичная сумма ![]() возрастает.
А из того, что последовательность частичных сумм возрастает и ограничена,
следует, что она имеет предел:
возрастает.
А из того, что последовательность частичных сумм возрастает и ограничена,
следует, что она имеет предел: ![]() , причём
, причём ![]() .
.
2) Пусть ряд
(*) расходится. Так как члены этого ряда положительны, то его частичная сумма ![]() возрастает с возрастанием
возрастает с возрастанием ![]() , и
, и ![]() .
Тогда в силу неравенства
.
Тогда в силу неравенства ![]() , получаем:
, получаем: ![]() , т.е. ряд (**) расходится.
, т.е. ряд (**) расходится.
В качестве ряда
для сравнения необходимо выбрать такой ряд, о котором заранее известно,
является ли он сходящимся или расходящимся. Примерами таких рядов являются:
ряд, представляющий сумму членов геометрической прогрессии 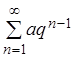 (см. разд. 2.1, пример 3), а также гармонический
(расходящийся) ряд.
(см. разд. 2.1, пример 3), а также гармонический
(расходящийся) ряд.
Пример 1. Исследовать на сходимость ряд:
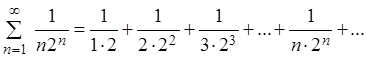
Решение. Для
того чтобы установить сходимость ряда, воспользуемся неравенством 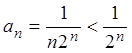
![]() и сравним данный ряд с
рядом
и сравним данный ряд с
рядом  . Ряд:
. Ряд: 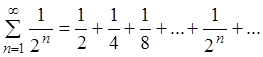 представляет
собой сумму бесконечно убывающей геометрической прогрессии с первым членом
представляет
собой сумму бесконечно убывающей геометрической прогрессии с первым членом  и знаменателем
и знаменателем 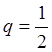 . Так
как
. Так
как 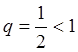 , то ряд
, то ряд  –
сходится. Согласно признаку сравнения (см. теорему 2.3), ряд
–
сходится. Согласно признаку сравнения (см. теорему 2.3), ряд  также сходится.
также сходится.
Чаще на практике бывает удобнее использовать признак сравнения в другой форме.
Теорема 2.4 (предельный
признак сравнения).Два ряда 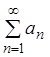 и
и ![]() с положительными членами одновременно
сходятся или одновременно расходятся, если существует конечный предел:
с положительными членами одновременно
сходятся или одновременно расходятся, если существует конечный предел: 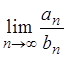 и
и 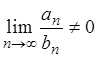 .
.
Пример 2.
Исследовать ряд: 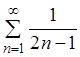 на сходимость.
на сходимость.
Решение. Общий
член данного ряда 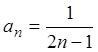 . Сравним ряд с расходящимся
гармоническим рядом:
. Сравним ряд с расходящимся
гармоническим рядом: ![]() , общий член которого
, общий член которого  . Далее, воспользуемся предельным признаком
сравнения (см. теорему 2.4):
. Далее, воспользуемся предельным признаком
сравнения (см. теорему 2.4):
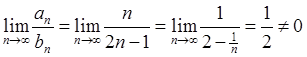 .
.
Отсюда следует,
что ряды: 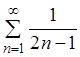 и
и ![]() одновременно
расходятся, т.е. ряд
одновременно
расходятся, т.е. ряд 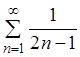 – расходящийся.
– расходящийся.
Теорема 2.5 (признак
Даламбера).Если все члены ряда 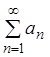 положительны
и
положительны
и
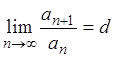 ,
(2.4)
,
(2.4)
то при ![]() ряд сходится, при
ряд сходится, при ![]() ряд
расходится (при
ряд
расходится (при ![]() ответа о сходимости ряда теорема
не даёт).
ответа о сходимости ряда теорема
не даёт).
Доказательство
1) Пусть ![]() и
и 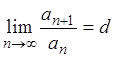 .
Докажем, что ряд
.
Докажем, что ряд 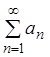 сходится. По определению предела
числовой последовательности для любого
сходится. По определению предела
числовой последовательности для любого ![]() существует
номер
существует
номер ![]() , такой, что при
, такой, что при ![]() выполняется
неравенство:
выполняется
неравенство: 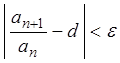 .
.
Отсюда следует, что  или
или
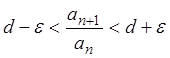 . (*)
. (*)
Так как ![]() , то
, то ![]() можно
взять настолько малым, что будет выполняться неравенство:
можно
взять настолько малым, что будет выполняться неравенство: ![]() . Полагая
. Полагая ![]() , где
, где ![]() , на основании правого из неравенств (*)
имеем:
, на основании правого из неравенств (*)
имеем:
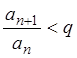 или
или ![]() для
для ![]()
Придавая ![]() значения
значения ![]() из
последнего неравенства получаем:
из
последнего неравенства получаем:
![]()
т.е. члены ряда
![]() (**)
(**)
меньше соответствующих членов ряда, составленного из членов геометрической прогрессии
![]() (***)
(***)
Так как ![]() , то ряд (***) сходится
(см. разд. 2.1, пример 2.3). Тогда согласно признаку сравнения ряд (**) также
сходится. Но ряд (**) получен из данного ряда
, то ряд (***) сходится
(см. разд. 2.1, пример 2.3). Тогда согласно признаку сравнения ряд (**) также
сходится. Но ряд (**) получен из данного ряда 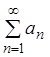 в
результате отбрасывания конечного числа первых членов, следовательно, ряд
в
результате отбрасывания конечного числа первых членов, следовательно, ряд 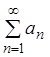 сходится.
сходится.
2) Пусть ![]() . Докажем, что ряд
. Докажем, что ряд 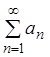 расходится. Возьмём
расходится. Возьмём ![]() настолько малым, чтобы
настолько малым, чтобы ![]() . Тогда при
. Тогда при ![]() в силу левого
из неравенств (*) выполняется неравенство:
в силу левого
из неравенств (*) выполняется неравенство: 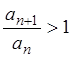 или
или ![]() . Таким образом, члены ряда, начиная с
некоторого номера
. Таким образом, члены ряда, начиная с
некоторого номера ![]() , возрастают с увеличением их
номеров, т.е. общий член ряда
, возрастают с увеличением их
номеров, т.е. общий член ряда ![]() не стремится к нулю при
не стремится к нулю при
![]() . Следовательно, согласно теореме 2.2 ряд
. Следовательно, согласно теореме 2.2 ряд 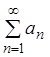 расходится.
расходится.
Замечание.
Как показывают примеры, при ![]() ряд
ряд 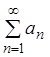 может как сходиться, так и расходиться. В
этом случае необходимо дополнительное исследование ряда с помощью признака
сравнения или других признаков.
может как сходиться, так и расходиться. В
этом случае необходимо дополнительное исследование ряда с помощью признака
сравнения или других признаков.
Пример 3.
Исследовать ряд ![]() на сходимость.
на сходимость.
Решение. Так
как 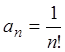 ,
, 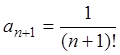 , то
, то


следовательно, ряд сходится.
Теорема 2.6 (радикальный признак Коши). Если все члены ряда 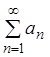 положительны и
положительны и
![]() (2.5)
(2.5)
то при ![]() ряд
сходится, при
ряд
сходится, при ![]() ряд расходится (при
ряд расходится (при ![]() теорема ответа
теорема ответа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.