Элементы химической термодинамики и кинетики, страница 5

В уравнении Аррениуса и, следовательно, всюду выше предполагается, что E не зависит от температуры. В действительности слабая зависимость все же существует. Значения энергии активации для гомогенных реакций в газовой фазе могут быть получены на основе теории строения молекул и статистической физики.

3.8 Кинетика сложных реакций

До сих пор мы говорили о простых реакциях, которые протекают в одну стадию. Описание кинетических закономерностей сложных реакций, т.е. протекающих в несколько стадий, во многом основано на кинетической теории простых реакций. Для простых реакций характерной является степенная зависимость скорости реакции от концентраций, в которой показатели степени - целые числа, совпадающие с абсолютными значениями стехиометрических коэффициентов. Скорости сложных реакций могут описываться самыми разнообразными зависимостями: степенными с произвольными показателями (дробными или целыми), зависимостями в виде дробных функций и т. д. Эти зависимости могут быть получены как чисто эмпирически, так и на основе анализа детального механизма реакции с использованием соотношений для скоростей простых стадий. Последний путь является более предпочтительным, так как позволяет установить более общие закономерности.

Продемонстрируем это на примере следующей реакции, для которой установлены все элементарные (простые) стадии:

- суммарная реакция

C₂H₆ + C₂H₄ ® CH₄ + C₃H₆;               r = ?

Элементарные стадии

С₂H₆ ↔ ˙CH₃ + ˙CH₃,            ;                (3.24)

˙CH₃ + С₂H₄ ® H˙+ C₃H₆,                 ;             (3.25)

H˙+ С₂H₆ ® CH₄ + ˙CH₃,                  ,             (3.26)

где ; ; ; ; ; .

В соответствии с (3.9)

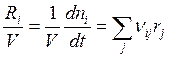, т.е. ; ; 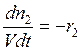; . И, следовательно, в соответствии с балансом молекул в суммарной реакции, необходимо, чтобы R₁ = R₂ = - R₃ = - R₄, т.е.

r₁ + r₃ = r₂ = r₃ = r₂.                                               (3.27)

Это возможно лишь, если r₁ = 0, т.е. , следовательно,

.

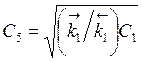Введя эту величину в r₂, получим

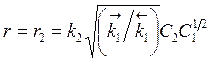.                                             (3.28)

Таким образом, соотношение для скорости сложной реакции получено теоретически благодаря знанию механизма реакции, при этом рассматриваемая сложная реакция имеет 1-й порядок по веществу A₂ и порядок 1/2 по A₁. Соотношения типа (3.28) - в виде произведения концентраций с различными показателями степени - имеют место обычно для гомогенных реакций. Для гетерогенных реакций (например, гетерогенного катализа) соотношения для скоростей реакции имеют еще более сложный вид.

3.9 Гетерогенный катализ. Теория Лэнгмюра-Хиншельвуда

Большинство современных химических процессов основано на применении катализаторов. Катализатором называется вещество, которое практически не расходуется в процессе химического превращения, а участвует в реакции лишь на промежуточных стадиях, изменяя маршрут реакции таким образом, чтобы обеспечивалось увеличение скорости образования целевого продукта в течение некоторого периода времени взаимодействия реакционной среды с катализатором. Оказывая влияние на скорость стадий, катализатор не оказывает влияния на химическое равновесие. В случае гетерогенного катализатора основные стадии химической реакции проходят на его поверхности. Именно поэтому катализаторами являются пористые материалы с развитой внутренней поверхностью.

Большинство современных подходов к описанию кинетических закономерностей протекания гетерогенно-каталитических реакций базируется на теории Лэнгмюра-Хиншельвуда, в основе которой лежит понятие «активного центра», впервые введенное Тэйлором.

Принимается, что активные центры распределены по поверхности катализатора равномерно. Активной является как внешняя поверхность частиц катализатора, так и поверхность пор. Число активных центров катализатора пропорционально его поверхности. Площадь поверхности пропорциональна массе катализатора или объему слоя катализатора, что эквивалентно тому, что поры распределены в объеме катализатора также равномерно. Скорость реакции может быть, следовательно, отнесена к массе, объему или поверхности катализатора. Очевидно, что определенные таким образом удельные скорости будут отличаться на постоянные коэффициенты.