Фундаментальные уравнения математических моделей химических реакторов

4 Фундаментальные уравнения математических моделей химических реакторов. 36

4.1 Основные уравнения. 36

4.1.1 Уравнение сохранения импульса. 37

4.1.2 Уравнения неразрывности и энергии. 37

4.2 Вопросы, исследуемые на основе математического моделирования. 42

4 Фундаментальные уравнения математических моделей химических реакторов

4.1 Основные уравнения

Наиболее эффективный метод моделирования химических реакторов основан на использовании концепции непрерывных взаимопроникающих континуумов, в соответствии с которой каждый компонент (а для многофазных реакторов и каждая фаза) рассматривается как непрерывная среда, распределенная по всему объему реакционного пространства и характеризующаяся собственной скоростью, плотностью, концентрациями, температурой и т.д.

Фундаментальными уравнениями математических моделей однофазных химических реакторов являются традиционные для механики сплошных сред дифференциальные уравнения, выражающие баланс массы (уравнение неразрывности), энергии и импульса для элементарного объема реакционной среды (реактора). Специфика анализа химического реактора состоит в том, что приходится анализировать взаимное превращение различных компонентов среды. Для этого в рассмотрение вводятся уравнения неразрывности для каждого компонента (континуума) с учетом обмена веществом между континуумами-компонентами в результате химической реакции (см. ниже (4.1)).

4.1.1 Уравнение сохранения импульса

В общей формулировке - это известное уравнение Навье-Стокса. При моделировании химических реакторов, как правило, рассматриваются более простые варианты этого уравнения или готовые решения, позволяющие определить перепад давления, распределение скоростей в реакторе и т.д. Вопрос о выборе упрощенного уравнения целесообразно обсуждать отдельно в каждом конкретном случае.

4.1.2 Уравнения неразрывности и энергии

Рассмотрим однофазный реактор. Для элементарного реакционного объема этого реактора (рис.4.1) можно записать следующие уравнения, выражающие баланс массы и энергии для каждого компонента, соответственно:

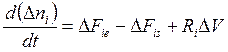, (i, … S)                          (4.1)

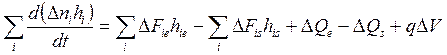, (i, … S),                  (4.2)

где  - число молей вещества A_i в элементарном объеме ; t - текущее время;  и  - входящий и покидающий элемент  молярные потоки компонента A_i соответственно; R_i - интенсивность объемных источников (стоков) вещества A_i за счет обмена между средами-компонентами в результате химической реакции (; см. (3.9)) или за счет распределенного по объему ввода (вывода) компонента A_i; , ,  - энтальпия образования одного моля содержащегося в , входящего в  и выходящего из  вещества A_i, соответственно; ,  - тепло, поступающее в элемент и выходящее из него за счет теплопроводности; q - интенсивность объемных источников (стоков) тепла на единицу объема реакционной среды (например, за счет обмена с внешним по отношению к реакционной среде теплоносителем, циркулирующим в размещенном в реакционном объеме теплообменнике (;  - величина площади теплообменной поверхности на единицу объема реактора в элементе ; k_f- коэффициент теплопередачи;  - температурный перепад реакционная среда/теплоноситель).

В уравнениях (4.1) или (4.2) первый член представляет собой скорость изменения количества вещества A_i (или энтальпии) в элементарном объеме , второй и третий - количества вещества A_i (или энтальпии), поступающих в  и выходящих из  в единицу времени соответственно за счет конвективного движения и/или диффузии (или теплопроводности), четвертый член - количество вещества, поступающего в  в единицу времени из внешней по отношению к рассматриваемому компоненту среды за счет объемных источников (или энтальпии, поступающей в реакционный объем за счет объемных источников из внешней среды).

Вместо (4.1) можно получить уравнение баланса массы в дифференциальной форме на основе следующих соображений.

Если рассматривать произвольный объем , ограниченный поверхностью , а удельный мольный поток массы, пронизывающий поверхность dS, характеризовать некоторой векторной величиной , то для такого объема можно записать

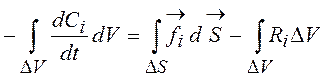, (i, … S)                                (4.3)

где , .

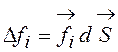Учитывая, что для любой векторной величины , в соответствии с формулой Гаусса-Остроградского,

,

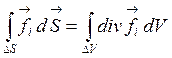(4.3) можно переписать в виде

.

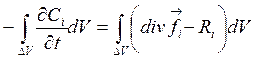Или с учетом того, что объем  произвольный

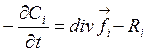.                                                     (4.4)

Для пространственных координат z1, z2, z3 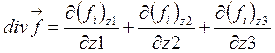 и, следовательно, (4.4) можно представить в виде

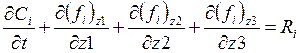.                                      (4.5)

Или в одномерном случае (, )

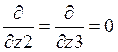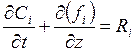.                                                        (4.6)

Если вместо удельного потока f_i, оперировать с величиной суммарного молярного потока через сечение аппарата , где  - площадь поперечного сечения реактора, то последнее соотношение лучше представлять в виде

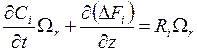.                                             (4.6 а)

Молярный поток  (моль/с) представляет собой сумму различных составляющих. В большинстве случаев можно ограничиться составляющими, обусловленными конвективным движением со скоростью u (обозначим его через F) и диффузией (по закону Фика молярный диффузионный шток ). При этом под  будем понимать эффективный коэффициент диффузии, включающий как молекулярную, так и турбулентную составляющие. В этом случае можно записать

.                                  (4.7)

С учетом (4.7) уравнение (4.6) можно переписать в виде

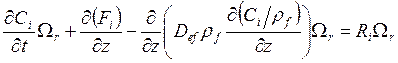.                     (4.8)