6 Однофазный проточный реактор идеального перемешивания (backmix reactor) 61
6.1 Уравнения баланса массы и энергии. 62
6.2 Некоторые частные случаи. 63
6.2.1 Сложная реакция первого порядка (ν1А1 + ν2А2 = 0, r = kC1s) 63
6.2.2 Две параллельные реакции первого порядка (ν11А1 + ν21А2 = 0, r1 = k1C1s; ν12А1 + ν32А3 = 0, r2 = k2C1s) 63
6.2.3 Две последовательные реакции первого порядка (ν11А1 + ν21А2 = 0, r1 = k1C1s; ν22А2 + ν32А3 = 0, r2 = k2C2s) 64
6.2.4 Кинетика Лэнгмюра-Хиншельвуда (А1 ® А2, r = - R = kC1s / (1 + AC1s)2) 65
6 Однофазный проточный реактор идеального перемешивания (Backmix reactor)
Принципиальные схемы реакторов рассматриваемого типа практически не отличаются от схем периодических реакторов (рис. 5.1). Необходимо лишь иметь в виду, что в рассматриваемом случае загрузка, и выгрузка реагентов и продуктов осуществляется непрерывно.
Под реактором идеального перемешивания понимают проточный (открытая термодинамическая система) реактор, в котором благодаря интенсивному перемешиванию обеспечивается постоянство температуры и концентрации по реакционному объему, т.е. в одномерном случае
![]() ,
, ![]() . (6.1)
. (6.1)
Будем считать, что реакционная система характеризуется стехиометрическим уравнением (5.1)
![]() ,
, ![]()
(![]() ,
, ![]() ,
, ![]() - для вещества, не участвующего в реакции).
- для вещества, не участвующего в реакции).
В реактор непрерывно
подаются исходные вещества ![]() и отводятся продукты
реакции
и отводятся продукты
реакции ![]() .
.
6.1 Уравнения баланса массы и энергии
Уравнения баланса массы и энергии, как и в п. 5.1, можно получить,
интегрируя уравнения (4.8) - (4.9) по всему реакционному объему (т. е. от z= 0 до z = Z). Для стационарных
условий (![]() ), если при этом учесть условия (6.1), а
также, что при z = 0
), если при этом учесть условия (6.1), а
также, что при z = 0 ![]() ,
, ![]() ,
при z = Z
,
при z = Z ![]() ,
, ![]() можно
получить следующие уравнения баланса массы и энергии:
можно
получить следующие уравнения баланса массы и энергии:
![]() ; (6.2)
; (6.2)
![]() . (6.3)
. (6.3)
Согласно (2.7) ![]() . Учитывая далее (5.1), а также что
. Учитывая далее (5.1), а также что ![]() из (6.2) и (6.3)
можно получить
из (6.2) и (6.3)
можно получить ![]()
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
или
![]() , (6.6)
, (6.6)
где учтено, что ![]() , Fi– мольный расход i-го вещества, моль/с.
, Fi– мольный расход i-го вещества, моль/с.
Первый член в (6.6) связан с различием температур входящего в
реактор и выходящего из реактора потоков: ![]() ,
второй - с тепловым эффектом реакции, третий - с энергообменом с внешней средой
(см. (5.37)).
,
второй - с тепловым эффектом реакции, третий - с энергообменом с внешней средой
(см. (5.37)).
Уравнения (6.4), (6.6) могут быть решены относительно ![]() и Тs. Для этого необходимо
знать все параметры реакционной среды (
и Тs. Для этого необходимо
знать все параметры реакционной среды (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) и реактора (V, kf,
) и реактора (V, kf, ![]() ,
Tmf).
,
Tmf).
Наиболее простые случаи:
Изотермический реактор: т = тs, тs - известна и независима от процесса. В этом случае решаются только уравнения (6.4).
Адиабатический реактор: qV = 0. В этом случае из уравнения (6.6) получаем
![]() ; (6.7)
; (6.7)
![]() . (6.8)
. (6.8)
Чтобы выразить все через концентрации необходимо помнить, что
![]() ,
, ![]() , (6.9)
, (6.9)
Fs, Fe- объемные расходы смеси (![]() ), м3/с, Vm – объем одного моля.
), м3/с, Vm – объем одного моля.
6.2 Некоторые частные случаи
Будем полагать, что температура в реакторе известна и равна Тs, кроме того, Fs = Fe= F (реакция без изменения объема). Порядок реакции и стехиометрические коэффициенты определяются независимо (закон действия масс не обязательно выполнятся).
6.2.1 Сложная реакция первого порядка (ν1А1 + ν2А2 = 0, r = kC1s)
В этом случае (см. (6.9))
![]() ,
, ![]() ,
поэтому (6.4) можно переписать в виде
,
поэтому (6.4) можно переписать в виде
![]() . (6.10)
. (6.10)
Или
![]() , (6.11)
, (6.11)
где ![]() -
среднее время пребывания реагента в реакторе.
-
среднее время пребывания реагента в реакторе.
![]() . (6.12)
. (6.12)
6.2.2 Две параллельные реакции первого порядка (ν11А1 + ν21А2 = 0, r1 = k1C1s; ν12А1 + ν32А3 = 0, r2 = k2C1s)
В этом случае на основании (6.4), (2.7), можно получить
![]() ;
; ![]() ; (6.13)
; (6.13)
![]()
и, так как
![]() ,
,
![]() , то
, то ![]() , откуда
, откуда ![]() . (6.14)
. (6.14)
Из (6.13) с учетом (6.14) можно получить
![]() ;
;
![]() . (6.15)
. (6.15)
Аналогично
![]() ,
, ![]() .
.
Конверсия
![]() . (6.16)
. (6.16)
Селективность
![]() , и так как
, и так как
![]()
(в идеале 2-я реакция протекать не должна, а на образование ν21 молей А2 расходуется ν11 молей А1),
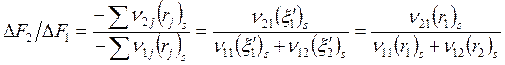 , следовательно,
, следовательно,
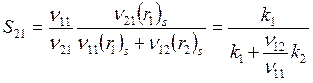 . (6.17)
. (6.17)
Выход
![]() . (6.18)
. (6.18)
6.2.3 Две последовательные реакции первого порядка (ν11А1 + ν21А2 = 0, r1 = k1C1s; ν22А2 + ν32А3 = 0, r2 = k2C2s)
![]() ;
; ![]() ;
;
![]() ;
;
![]() , откуда
, откуда
![]()
![]() (6.19)
(6.19)
или в терминах химической переменной
![]() ;
;
![]() . (6.20)
. (6.20)
Конверсия
![]() . (6.21)
. (6.21)
Селективность
![]()
и так как ![]() (в идеале 2-я реакция протекать не должна, а на
образование ν21 молей А2
расходуется ν11 молей А1),
(в идеале 2-я реакция протекать не должна, а на
образование ν21 молей А2
расходуется ν11 молей А1),
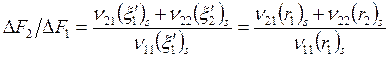 ;
;
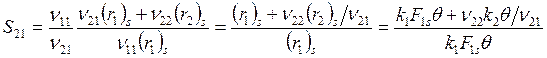 , откуда после подстановки F1s и F2s
, откуда после подстановки F1s и F2s
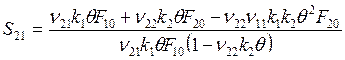 . (6.22)
. (6.22)
Выход
![]()
В случае F20 = 0
![]()
или
![]() ,
, 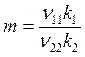 . (6.23)
. (6.23)
6.2.4 Кинетика Лэнгмюра-Хиншельвуда (А1 ® А2, r = - R = kC1s / (1 + AC1s)2)
В соответствии с (6.2) можно записать
![]() .
.
Или, вводя подстановки ![]() ,
, ![]() ,
,
![]() . (6.24)
. (6.24)
Из рассматриваемого
примера видно, что вид кинетического уравнения может определять множественность
решений. Действительно, уравнение (6.24) третьей степени относительно ![]() и может иметь три решения. Графически -
это точки пересечения зависимостей
и может иметь три решения. Графически -
это точки пересечения зависимостей ![]() и
и ![]() . Эти зависимости изображены на рис. 6.1.
Из рисунка видно, что решения S1 и S3 - устойчивы, а S2 - неустойчивое.
Действительно, при отклонении
. Эти зависимости изображены на рис. 6.1.
Из рисунка видно, что решения S1 и S3 - устойчивы, а S2 - неустойчивое.
Действительно, при отклонении ![]() вправо от S1
вправо от S1 ![]() (расход реагента в реакции превосходит его
приход с потоками), следовательно,
(расход реагента в реакции превосходит его
приход с потоками), следовательно, ![]() начнет
уменьшаться и происходит возвращение к S1. При отклонении влево
начнет
уменьшаться и происходит возвращение к S1. При отклонении влево ![]() от точки S1, реагент будет
накапливаться,
от точки S1, реагент будет
накапливаться, ![]() возрастать, т.е. возвращаться к S1. Аналогично поведение
системы в окрестности точки S3. В окрестности же точки S2 любое отклонение только
возрастает, т.е. режим неустойчив.
возрастать, т.е. возвращаться к S1. Аналогично поведение
системы в окрестности точки S3. В окрестности же точки S2 любое отклонение только
возрастает, т.е. режим неустойчив.
В зависимости от относительного расположения кривой ![]() и прямой
и прямой ![]() число
решений может быть меньше трех. В ситуации, когда имеют место решения
число
решений может быть меньше трех. В ситуации, когда имеют место решения ![]() ,
, ![]() , общее
число решений равно 2.
, общее
число решений равно 2.
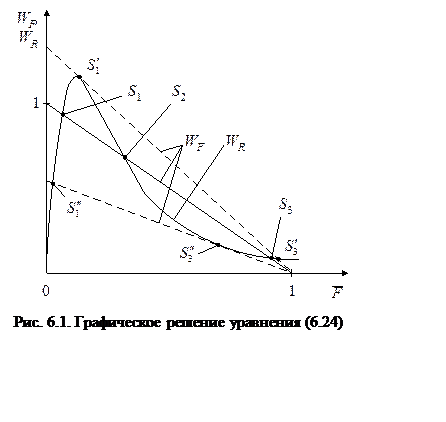 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.