Фундаментальные уравнения математических моделей химических реакторов, страница 2

Из (4.2) аналогично можно получить уравнение баланса энергии для одномерного случая

, (i, … S)                (4.9)

При выводе (4.9) было учтено, что , , т.е. , а для одномерного случая (, 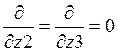)  ( - эффективный коэффициент теплопроводности). Кроме того для упрощения уравнения принято, что , так как теплоперенос в результате диффузии вещества мал вследствие того, что в (4.2) производится суммирование по всем компонентам A_i. И так как суммарный диффузионный поток по всем компонентам равен нулю, то слагаемые под знаком суммы, содержащие  (см. (4.7)) для различных компонентов, в существенной степени компенсируют друг друга.

Если же учесть, что ,  - мольная теплоемкость вещества A_i (по определению), (4.8) и (4.9) можно переписать в терминах скорости и теплоемкости:

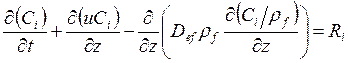,                  (4.10)

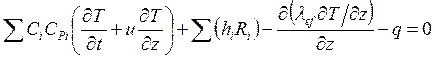,              (4.11)

При выводе (4.11) учтено, что

,

, т.е. что

;                                       (4.12)

.                                       (4.13)

Полученные уравнения (при наличии соответствующих замыкающих уравнений и начальных и граничных условий) позволяют рассчитывать необходимые характеристики реактора и реализуемого в нем процесса.

Замыкающие уравнения представляются соотношениями для постоянных или переменных входящих в уравнения (4.1) - (4.11) коэффициентов, которые могут быть получены теоретически или экспериментально независимо от протекающего в реакторе процесса. Таковыми являются, например, уравнения состояния газа, соотношения для теплофизических свойств среды, скоростей реакций и др.

Начальные и граничные условия отражают конкретные особенности того или иного реактора и технологического процесса, их целесообразно формулировать специально в каждом конкретном случае.

Специфической особенностью математических моделей химических реакторов является сильная нелинейность дифференциальных уравнений, обусловленная прежде всего экспоненциальной зависимостью (3.17) константы скорости реакции от температуры. Полезным упрощением температурной зависимости (хотя и не приводящим к линеаризации дифференциальных уравнений) является предложенное Франк-Каменецким преобразование, заключающееся в линеаризации показателя экспоненты в окрестности некоторой температуры отсчета Т₀ на основе разложения 1/Т в ряд Тейлора

Подстановка этого приближения в (3.15) дает

,                                      (4.14)

где показатель степени является линейной функцией Т.

Многофазные реакторы являются существенно более сложными объектами для анализа. В рамках концепции взаимопроникающих континуумов в случае многофазных реакторов уравнения типа (4.1), (4.11) записываются для каждой фазы, при этом в уравнениях появляются дополнительные члены, отражающие наличие взаимодействия фаз путем обмена между фазами веществом, энергией и импульсом. Обычно эти члены отражены в уравнениях в виде дополнительных соотношений для интенсивности объемных источников или стоков (например, интенсивность поступления вещества из одной фазы в другую на единицу объема).

4.2 Вопросы, исследуемые на основе математического моделирования

Современный уровень вычислительной техники позволяет решать на основе математического моделирования самые разнообразные задачи анализа химических реакторов: от анализа отдельных эффектов в пределах химического реактора, до оптимизации химико-технологических систем, в которых сам химический реактор выступает в качестве внутреннего элемента системы.

В данном пособии акцентируется внимание на общей методологии анализа химических реакторов и рассмотрении наиболее значимых с точки зрения работы реактора вопросов на примерах анализа некоторых характерных типов реакторов и процессов.

К типичным вопросам, исследуемым на основе математического моделирования, можно отнести следующие:

- интегральные показатели работы реактора (степень превращения, селективность, выход) в зависимости от типа реактора, режимных параметров, кинетики реакции (соотношения для скорости реакции, порядка реакции, числа реакций, их последовательности), структуры фаз, интенсивности межфазного взаимодействия;

- интегральные показатели работы реактора в зависимости от распределения температуры, оптимальное распределение температуры;

- факторы и методы воздействия на температурный режим реактора;

- анализ влияния особенностей межфазного взаимодействия на эффективность работы реактора;

- выбор оптимальной конструкции и режима работы реактора;

- параметрическая чувствительность (чувствительность изменения показателей работы реактора в зависимости от изменения свойств реакционной среды - параметров модели; например, изменение температуры или конверсии, или селективности при изменении теплоты реакции и неизменных прочих условиях);

- множественность и устойчивость стационарных режимов работы реактора;

- динамика химического реактора (пусковые и переходные режимы, релаксация возмущающих воздействий, автоколебания).

В общем случае анализ этих вопросов базируется на использовании численных методов решения систем нелинейных дифференциальных уравнений в частных производных, теории анализа устойчивости стационарных решений и других специальных математических методов, обсуждение или применение которых выходит за рамки данного пособия. Ниже будут рассмотрены относительно простые одномерные модели, допускающие, как правило, аналитические решения и дающие, тем не менее, достаточно полное представление о методологии анализа химических реакторов.