Контрольная работа на тему «Расчёт параметров работы службы с клиент-серверной технологией»
Исходные данные:
1. Количество абонентов сети: nаб = 100 + 15К = 100 + 15 · 6 = 190, где К – последняя цифра студенческого билета (6). Число абонентов в сети растет на 15% с каждым годом.
2. Интенсивность запросов абонентов в пик наибольшего обращения составляет 20% от общего числа клиентов.
3. Возможности сервера. Среднее время обслуживания каждого запроса Тs = 0,13 с.
4. Закон распределения времени обслуживания запросов сервером неизвестен.
Расчету подлежат следующие величины и их динамика по годам (сроком до пяти лет):
1. Утилизация сервера – r (доля времени, в течение которого он работает, с учётом простоев из-за возможных промежутков в поступлении запрсов).
2. Размер очереди – w.
3. Количество элементов, одновременно находящихся в системе – q.
4. Среднее время ожидания очереди – Тw.
5. Среднее время обработки запроса системой (время реакции системы на запрос) – Тq.
Решение. Закон распределения времени обслуживания запросов сервером неизвестен, можно создать имитационную математическую модель сети и проанализировать в разных условиях. Рассчитаем параметры для трех наиболее распространенных законов распределения (формулы приведены в таблице 1). В качестве оценок выбираем наихудшие значения из рассчитанных.
Утилизация сервера рассчитывается по формуле:
![]() , [запросов] (1)
, [запросов] (1)
где λS – интенсивность поступления запросов в систему; ТS – среднее время обслуживания запроса сервером.
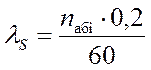 ,
[запросов/сек] (2)
,
[запросов/сек] (2)
где nабi – число абонентов в i-ом году.
![]() . (3)
. (3)
Таблица 1
Нормальный |
Экспоненциальный |
Равномерный |
|
M/G/1 |
M/M/1 |
M/D/1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчётов параметров односерверной системы представлены в таблицах 2 ÷ 5.
Таблица 2
|
Годы |
1 |
2 |
3 |
4 |
5 |
|
nабi |
190 |
219 |
247 |
276 |
304 |
|
λS |
0,63 |
0,73 |
0,82 |
0,92 |
1,013 |
|
ρi |
0,082 |
0,095 |
0,107 |
0,120 |
0,132 |
Таблица 3
|
Модель М/G/1 |
|||||
|
Годы |
1 |
2 |
3 |
4 |
5 |
|
q |
0,0859 |
0,1003 |
0,1138 |
0,1287 |
0,1427 |
|
ω |
0,0039 |
0,0053 |
0,0068 |
0,0087 |
0,0107 |
|
Тq |
0,1362 |
0,1373 |
0,1383 |
0,1394 |
0,1407 |
|
Тω |
0,0062 |
0,0073 |
0,0083 |
0,0094 |
0,0105 |
Таблица 4
|
Модель М/М/1 |
|||||
|
Годы |
1 |
2 |
3 |
4 |
5 |
|
q |
0,0893 |
0,1050 |
0,1198 |
0,1364 |
0,1521 |
|
ω |
0,0073 |
0,0100 |
0,0128 |
0,0164 |
0,0201 |
|
Тq |
0,1416 |
0,1437 |
0,1456 |
0,1477 |
0,1498 |
|
Тω |
0,0116 |
0,0137 |
0,0156 |
0,0177 |
0,0198 |
|
σq |
0,3119 |
0,3406 |
0,3663 |
0,3937 |
0,4186 |
|
σTq |
0,1543 |
0,1588 |
0,1631 |
0,1678 |
0,1726 |
Таблица 5
|
Модель М/D/1 |
|||||
|
Годы |
1 |
2 |
3 |
4 |
5 |
|
q |
0,0857 |
0,1000 |
0,1134 |
0,1282 |
0,1420 |
|
ω |
0,0037 |
0,0050 |
0,0064 |
0,0082 |
0,0100 |
|
Тq |
0,1358 |
0,1368 |
0,1378 |
0,1389 |
0,1399 |
|
Тω |
0,0058 |
0,0068 |
0,0078 |
0,0089 |
0,0099 |
|
σq |
0,0443 |
0,0489 |
0,0532 |
0,0579 |
0,0622 |
|
σTq |
0,0231 |
0,0253 |
0,0271 |
0,0291 |
0,0309 |
Из расчётов видно, что наихудшие параметры у системы с экспоненциальным распределением времени обслуживания, поэтому её параметры мы применяем в качестве оценочных.
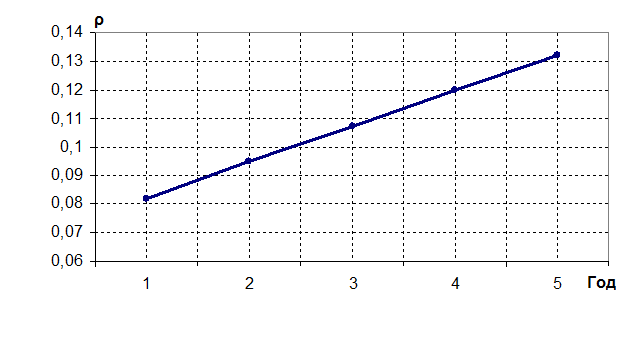
Рисунок 1 – Динамика роста утилизации сервера
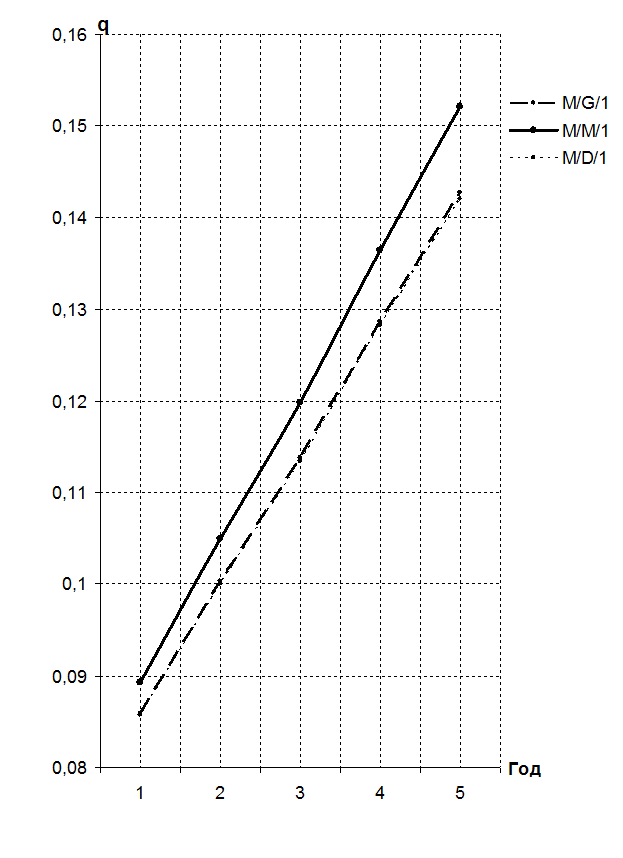
Рисунок 2 – Динамика роста числа элементов, одновременно находящихся в системе
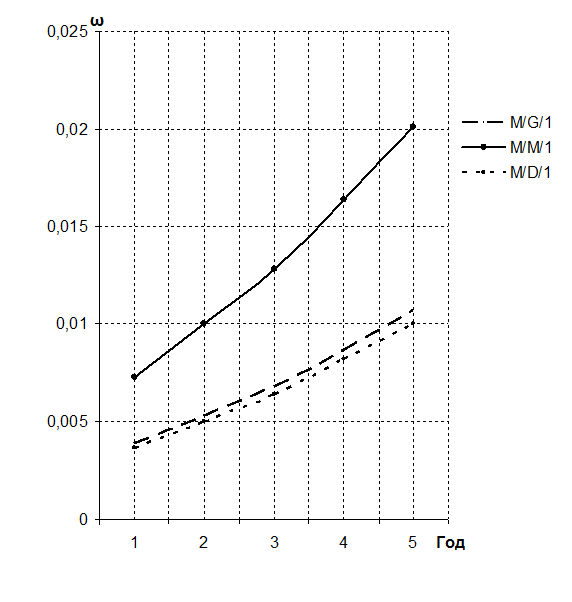
Рисунок 3 – Динамика роста размера очереди
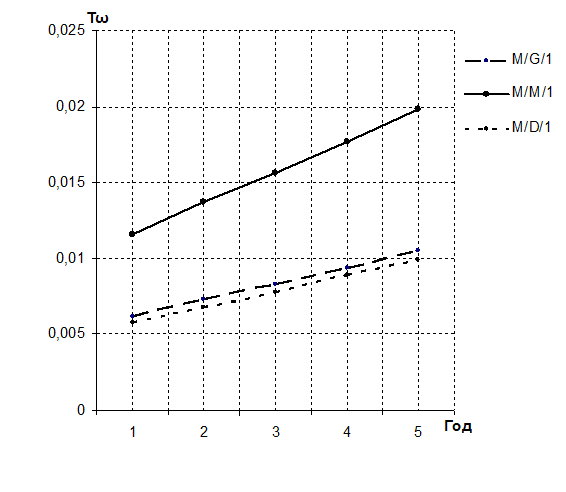
Рисунок 4 – Динамика изменения среднего времени ожидания обслуживания в очереди
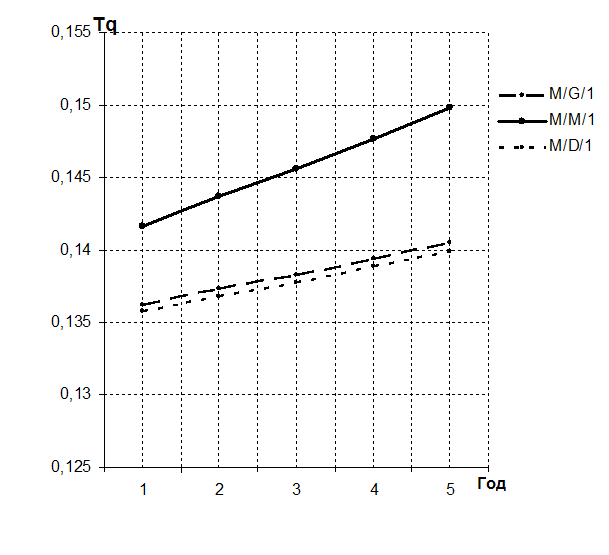
Рисунок 5 – Динамика изменения среднего времени обработки запроса для односерверной системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.