Расчет параметров работы службы с клиент-серверной технологией, страница 2

При большом количестве абонентов один сервер не обеспечивает требуемого качества обслуживания. В таком случае используется система из нескольких серверов. Расчёт многосерверной системы производим для случая с экспоненциальным законом распределения времени обслуживания. Время поступления заявок для всех серверов описывается распределением Пуассона, а время обслуживания заявок − экспоненциальным законом. Если в системе N идентичных серверов, а ρ – утилизация каждого сервера, то утилизация всей системы (интенсивность трафика):

.                                                           (4)

Для каждого сервера утилизация определяется по формуле:

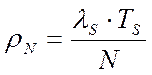;                                                       (5)

количество элементов, одновременно находящихся в многосерверной системе:

.                                                   (6)

Для расчёта других параметров используем формулы, содержащие функцию Эрланга, физический смысл которой – определение вероятности, что все серверы в определённый момент заняты (вероятность того, что количество запросов, находящихся в данный момент в системе, будет больше количества серверов):

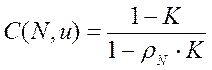,                                                     (7)

где К – коэффициент пуассоновского распределения:

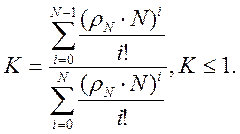                                                           (8)       

Математическое ожидание размера очереди (количество элементов в очереди) определяется по формуле:

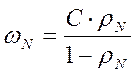;                                                            (9)

число элементов, находящихся в системе:

;                                                     (10)

среднее время ожидания обслуживания в очереди:

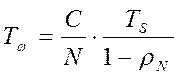;                                                      (11)

среднее время ожидания в системе:

.                                                         (12)

Результаты расчётов для 2-серверной системы представлены в таблице 6, для 3-серверной системы – в таблице 7.

Таблица 6

Годы	1	2	3	4	5
ρN	0,0410	0,0475	0,0533	0,0598	0,0659
ωN	1,37 · 10-4	2,14 · 10-4	3,04 · 10-4	4,33 · 10-4	5,72 · 10-4
qN	0,0821	0,0952	0,1069	0,1200	0,1324
Тω	0,0002	0,0003	0,0004	0,0005	0,0006
Тq	0,1302	0,1303	0,1304	0,1305	0,1306

Таблица 7

Годы	1	2	3	4	5
ρN	0,0273	0,0316	0,0355	0,0399	0,0439
ωN	2,81 · 10-6	3,36 · 10-6	7,62 · 10-6	13,01 · 10-6	14,42 · 10-6
qN	0,0819	0,0948	0,1065	0,1197	0,1317
Тω	4,46 · 10-6	4,61 · 10-6	9,30 · 10-6	14,13 · 10-6	14,23 · 10-6
Тq	0,130005	0,130005	0,130009	0,130014	0,130014

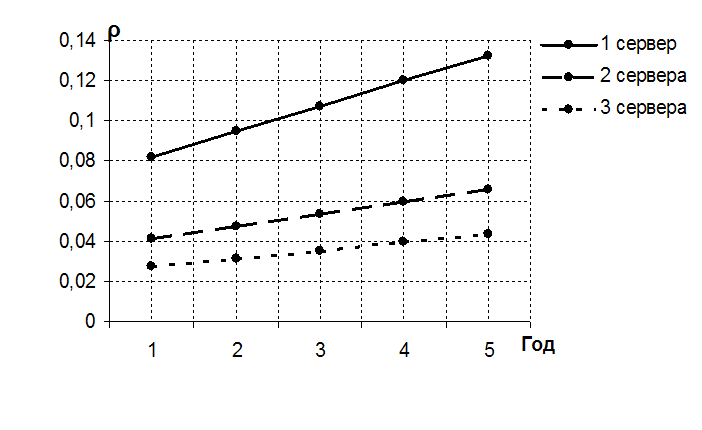
Рисунок 6 – Динамика роста утилизации одно-, двух-, трёхсерверной системы

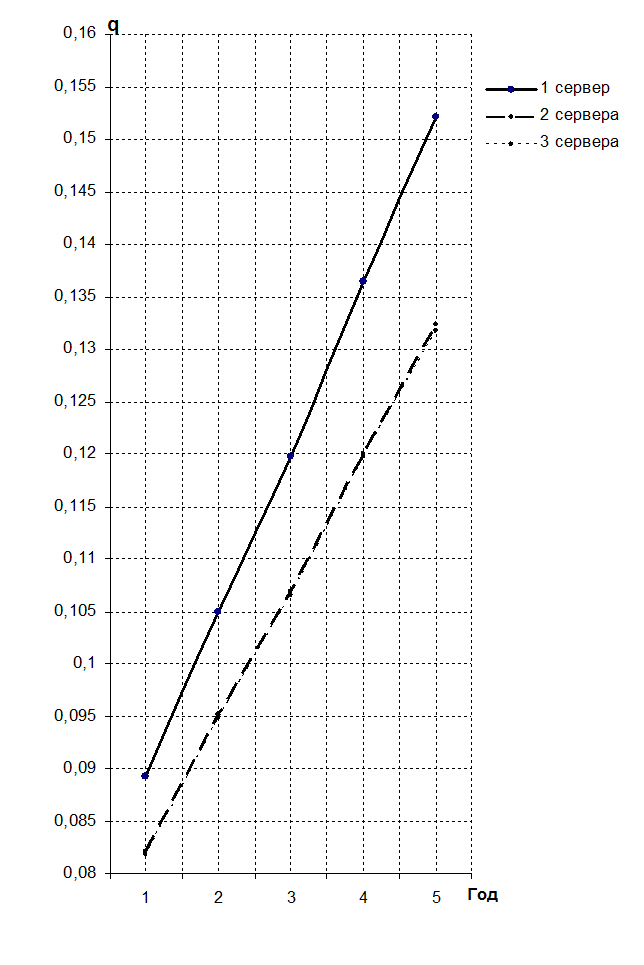
Рисунок 7 – Динамика роста числа элементов, находящихся в системе с одним, двумя и тремя серверами

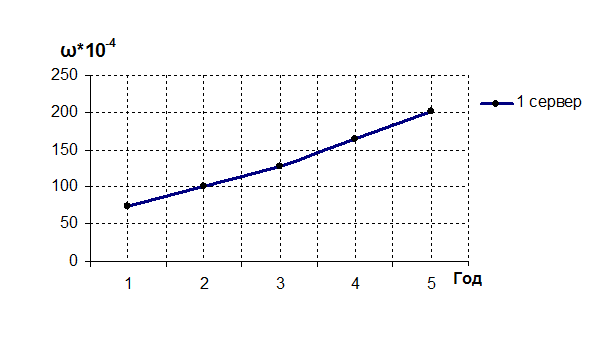
Рисунок 8 – Динамика роста размера очереди для односерверной системы

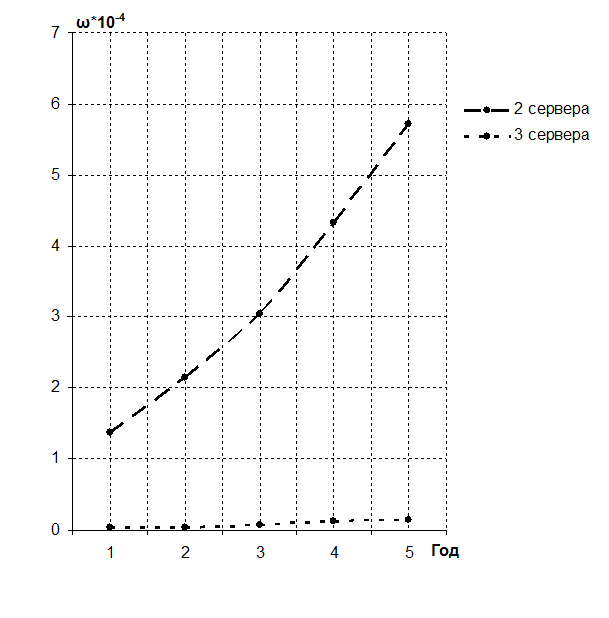
Рисунок 9 – Динамика роста размера очереди для двух- и трёхсерверной системы

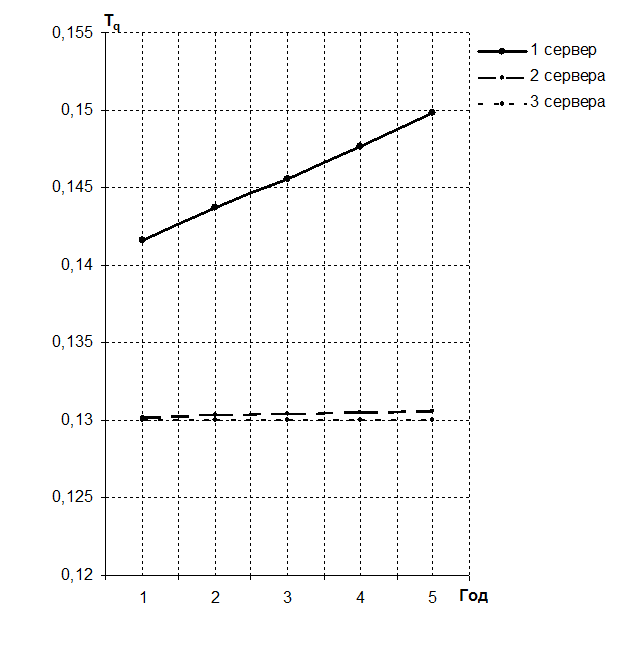
Рисунок 10 – Динамика изменения среднего времени обработки запроса для одно-, двух-, трёхсерверной системы

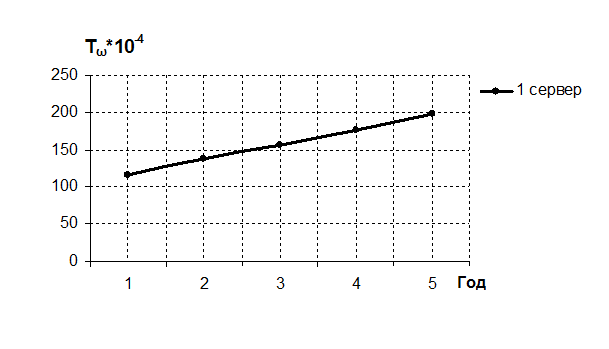
Рисунок 11 – Динамика изменения среднего времени ожидания обслуживания в очереди для односерверной системы

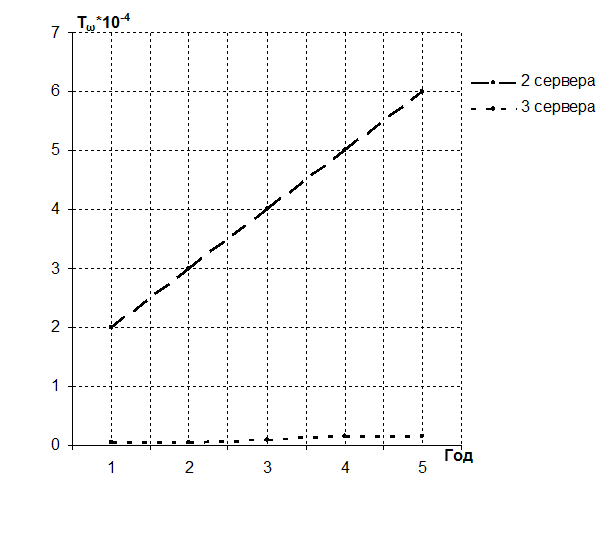
Рисунок 12 – Динамика изменения среднего времени ожидания обслуживания в очереди для двух- и трёхсерверной системы

Из графиков (рис. 11, 12) видно, что допустимое время ожидания обслуживания в очереди может обеспечиваться в системе с двумя и тремя серверами.

Определим, в скольких процентах случаев это время будет превышено. Для чего используем формулу математического ожидания времени ожидания в очереди:

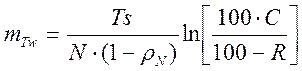,                                        (13)

где R – процент числа случаев, когда время ожидания не превышает это математическое ожидание:

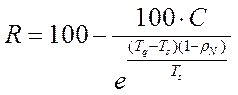 .                                          (14)

Учитывая выражение T_q = T_s + T_w ® T_w = T_q − T_s,  найдем, в скольких процентах случаев T_w не превысит допустимое значение.

Для двухсерверной системы:

.

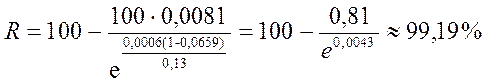Таким образом, в системе с двумя серверами время ожидания обслуживания выше нормы будет в 0,81% случаев, т.е. для 81-й заявки из 10 тысяч.

Для трёхсерверной системы:

.

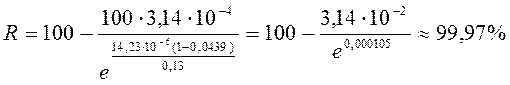Из расчётов видно, в системе с тремя серверами время ожидания обслуживания выше нормы будет в 0,03% случаях, т.е. для 3-х заявок из 10 тысяч, что является отличным показателем.

Список литературы

1.  Кох Р., Яновский Г.Г. Эволюция и конвергенция в электросвязи. – М.: Радио и связь, 2001. – 280 с.

2.  Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы. – Спб.: Питер, 2002. – 672 с.

3.  Телекоммуникационные системы и сети: Учебное пособие. Том 1 − Современные технологии/ Б.И. Крук, В.Н. Попантонопуло, В.П. Шувалов. – М.: Горячач линия – Телеком, 2003. – 647 с.