Синтез робототехнической системы из трех вращательных кинематических пар пятого класса

Санкт-Петербургский Государственный Университет

Информационных Технологий Механики и Оптики

Кафедра систем управления и информатики

Расчетно-графическая работа

по курсу " Робототехнические системы и комплексы"

Вариант 5

Выполнила: Наговицина Аня

   гр. 5146

Преподаватель: Котельников Ю.П.

Санкт-Петербург

2006 г.

1 ЗАДАНИЕ

Дана робототехническая система, кинематическая схема которой представлена на рисунке 1.

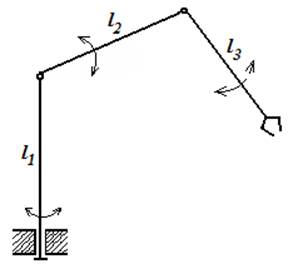
Рисунок 1 - Кинематическая схема робототехнической системы

Исходные данные:

                                

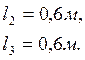
Основным вопросом при рассмотрении манипулирования с использованием роботов является способность поместить объект управления (схват манипулятора) в определенную точку с требуемой ориентацией в заданное время.

Прямая задача кинематики.

Определение  - вектора, определяющего положение схвата манипулятора, при известном векторе параметров :

,

.

Обратная задача кинематики.

Определение параметров  звеньев манипулятора, если известен вектор  - радиус вектор схвата.

Для решения прямой и обратной задач необходимо определенным образом осуществлять выбор систем координат.

2 ВЫБОР СИСЕМЫ КООРДИНАТ

Манипулятор представляет собой систему материальных тел (звеньев), образующих разомкнутую кинематическую цепь. Звенья этой цепи образуют 3 вращательных кинематических пары пятого класса.

Для того чтобы описать положение - го звена  в системе , свяжем с этим звеном декартову систему координат . В качестве основной системы обычно выбирается система , связанная со стойкой манипулятора. Ось  направим вдоль первого звена манипулятора. В качестве оси  выбирается перпендикуляр к оси , а направление задается так, чтобы система координат  была правой. При таком выборе систем координат каждая  - тая система координат связана с - тым звеном манипулятора.

Далее выбираем системы координат, руководствуясь следующими правилами выбора: ось  при совпадает с осью кинематической пары с тем же номером. Ось  для  определяется как общий перпендикуляр к осям  и  и имеет направление от  к . Ось для  выбирается так, чтобы система координат  была правой. Система координат  связывается со схватом манипулятора.

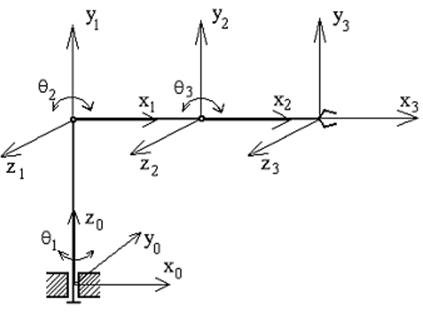
Рисунок 2 -  Выбор систем координат

         3 НАХОЖДЕНИЕ МАТРИЦ ПРЕОБРАЗОВАНИЙ КООРДИНАТ

Обозначим угол поворота i-го звена относительно (i-1)-го через. Совокупность величин    однозначно определяют положение механизма в пространстве. Эти величины названы обобщенными координатами механизма и обозначаются вектором , причем , где   - для вращательной кинематической пары.

Для определения матриц перехода из i-ой в (i-1)-ую систему координат необходимо найти следующие величины: , , , . Для этого совместим систему  с системой  посредством следующих последовательно выполняемых операций:

а) поворот на угол   вокруг оси  до тех пор, пока оси  и  не станут параллельными;

б) перенос на величину  вдоль оси  до тех пор, пока оси  и  не совместятся;

в) перенос на величину   вдоль оси  до совпадения начала координат  с началом координат ;

г) поворот на угол  относительно оси  до совмещения всех координатных осей.

Из четырёх параметров , , , , определяющих переход от одной системы координат к другой, параметры  и  всегда постоянны и определяются конструктивными особенностями звеньев. Из двух других параметров (, ) один является переменным и совпадает с обобщённой координатой, соответствующей (i-1)-ой кинематической паре; другой параметр постоянен: для вращательной кинематической пары, для поступательной кинематической пары .

Общий случай матрицы преобразования из (i-1)-ой системы координат в i-ую:

.

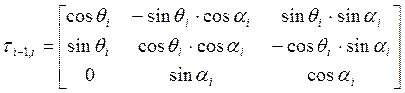1)  Перехода из СК   в СК : .

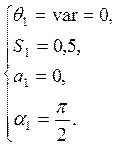Матрица преобразования координат: , , .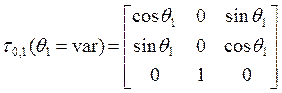

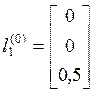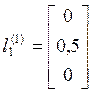2)  Перехода из СК   в СК : .

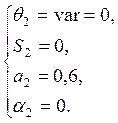Матрица преобразования координат: , , .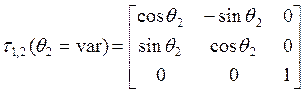

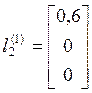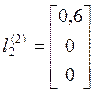3)  Перехода из СК   в СК : .

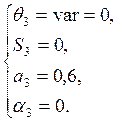Матрица преобразования координат: , , .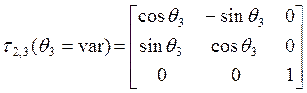

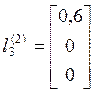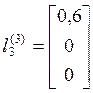         4 РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ КИНЕМАТИКИ

Вектор, определяющий положение схвата манипулятора:

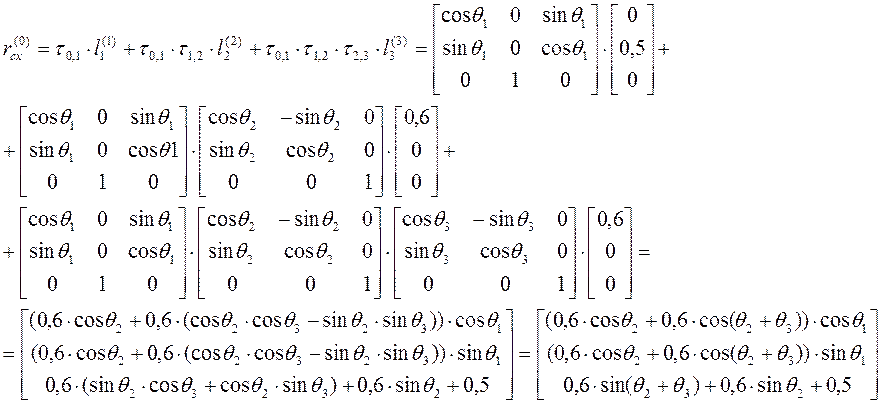
Выполним проверки:

1) Пусть ,,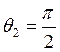, т.е. манипулятор выставлен   вертикально вверх в абсолютной системе координат – все три плеча манипулятора будут  проектироваться на ось z₀. Тогда подставляя в выражение для значения углов поворота, получим:

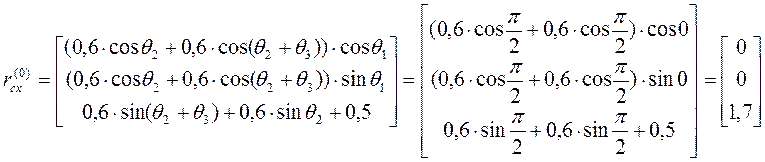(верно).

2) Пусть ,,,  т.е. манипулятор находится в исходном положении (рисунок 2) – плечо 1 манипулятора будет  проектироваться на ось z₀, а плечи 2 и 3 – на ось x₀. Тогда подставляя в выражение для значения углов поворота, получим:

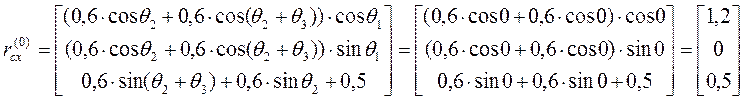(верно).

3) Пусть 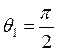,,, 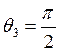т.е. плечо 1 повернуто относительно оси вращения на 90⁰(проектируется на ось z₀),  плечо 2 в исходном положении (проектируется на ось y₀), а плечо 3- повернуто вверх на 90⁰ (проектируется на ось z₀₎. Подставляя в выражение для значения углов поворота, получим:

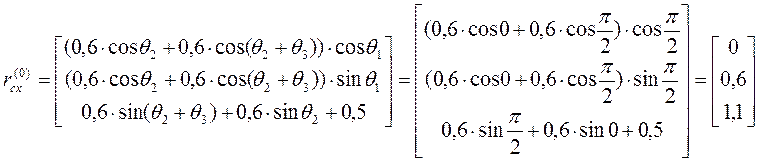 (верно).

Результаты проверки подтверждают правильность выбора систем координат и расчетов.