Синтез робототехнической системы из трех вращательных кинематических пар пятого класса, страница 2

5 УРАВНЕНИЕ ДИНАМИКИ ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА

Динамику исполнительного механизма промышленного робота состоящего из кинематических пар пятого класса, относительно инерционной системы координат , связанной со стойкой манипулятора. Полное уравнение динамики, описывающее движение манипулятора под действием приложенных внешних сил , моментов  и сил тяжести представимо в виде:

, где  - блочные векторы размера  сил тяжести, внешних сил и моментов; - момент на выходе механизмов передачи движения, вектор-столбец  вида .  - блочные матрицы , зависящие от пространственного положения, от параметров, скорости, связанной со стойкой манипулятора.

Для кинематической схемы (задана в Т.З.) будем считать, что рабочая среда организована т.о., что внешние моменты и силы отсутствуют, т.е.  и . Пренебрежем членом , тогда матричное уравнение, описывающее динамику исполнительного механизма примет вид:

.

Таким образом для описания динамических свойств исполнительного механизма, рассматриваемого манипулятора необходимо определить элементы матриц  и , а также

, где  - моменты, развиваемые приводами манипулятора в парах вращения; - силы, развиваемые приводами поступательных пар.

5.1 ПОСТРОЕНИЕ БЛОЧНЫХ МАТРИЦ

; ;

; ;

 ; ;

;

; ;;.

; ;;

; ; ; ;;

;

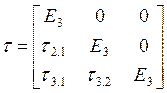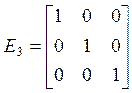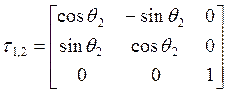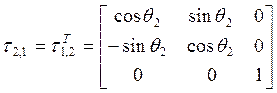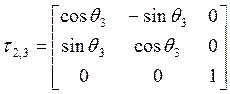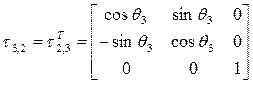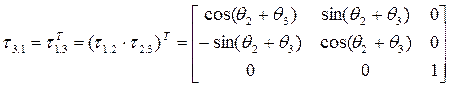
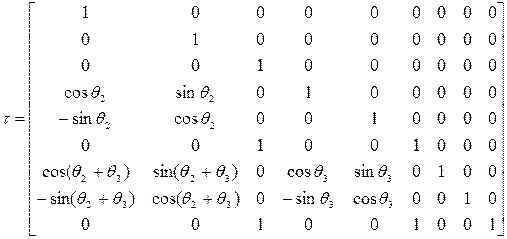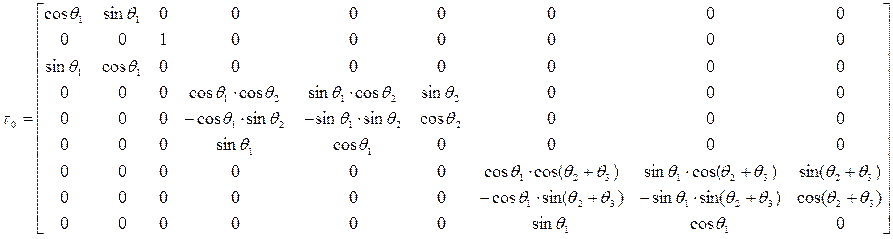
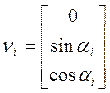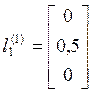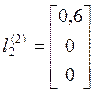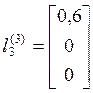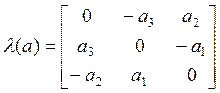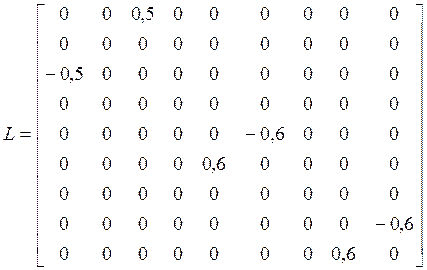Свяжем с каждым из звеньев манипулятора правую систему координат  таким образом, чтобы начало координат этой системы совпадало с центром масс  - го звена, а оси были параллельны осям системы координат .

Положение центра масс  - го звена в системе  определяется вектором .

Будем считать, что .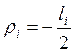

Тогда , ,;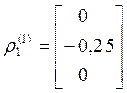

;

;

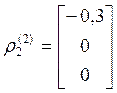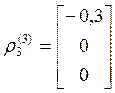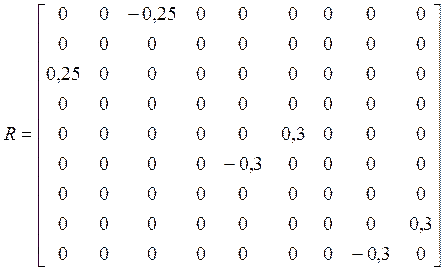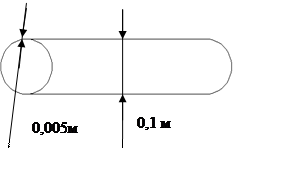
5.2 ОПРЕДЕЛЕНИЕ МАССЫ ЗВЕНЬЕВ

Будем считать, что каждое звено манипулятора представляет собой полый цилиндр диаметром 10 см и толщиной стенок 5 мм (см. рисунок 3).

Рисунок 3 -  Вид применяемых звеньев

Определим массу звеньев:

 ;

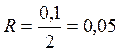, где  м, 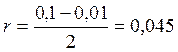 м, а - длина звена.

, тогда масса первого звена

,

, тогда масса второго звена

,

, тогда масса третьего звена

.

;

5.3 ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ

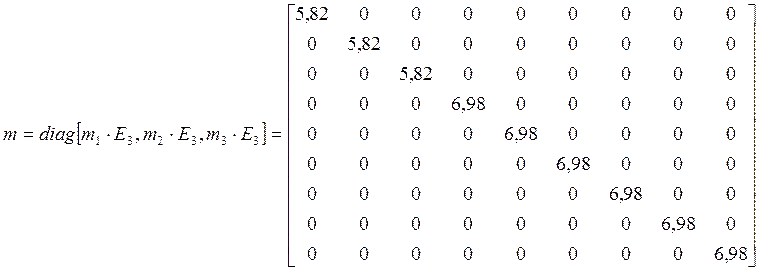Рассмотрим звенья в продольном направлении. Звенья представляют собой полые цилиндры с радиусами . Ось инерции совпадает с осью цилиндра, тогда .

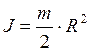В поперечном направлении представим звенья как прямые тонкие стержни длиной , массой, осью инерции перпендикулярной оси стержня и проходящей через его середину, тогда .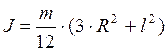

Первое звено:

;

.

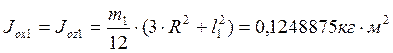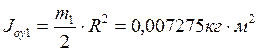Второе звено:

;

.

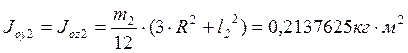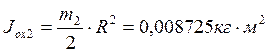Третье звено:

;

.

;

.

5.4  ВЫЧИСЛЕНИЕ МАТРИЦ А(q) и D(q)

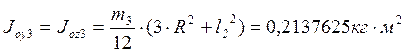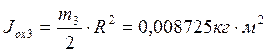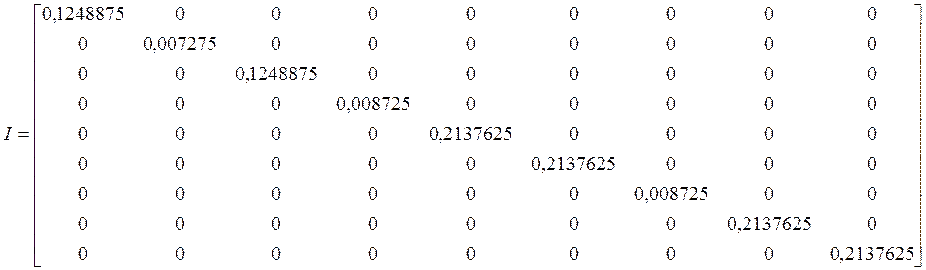
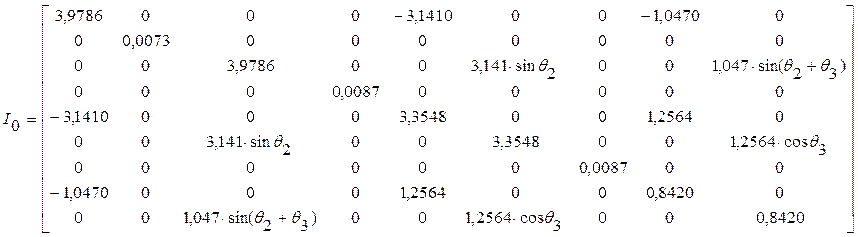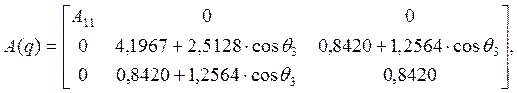 где

;

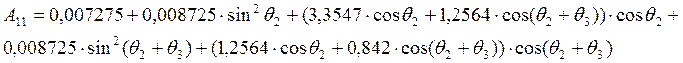
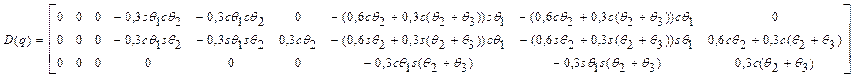
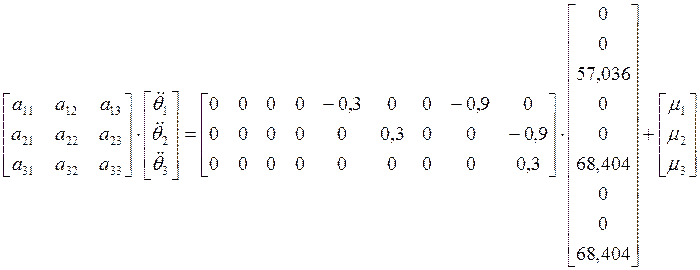Задав 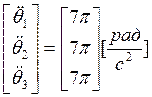, можно найти константы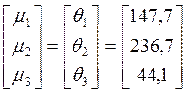

6 ВЫБОР ДВИГАТЕЛЕЙ

6.1 РАСЧЕТ ПРИВОДА

Зададим угловые скорость и ускорение нагрузки: , .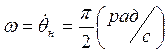

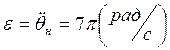1) Первый канал системы:

Требуемая мощность:

,

.

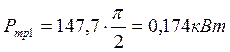2) Второй канал системы:

Требуемая мощность:

,

.

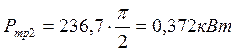3) Третий канал системы:

Требуемая мощность:

,

.

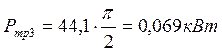6.2 ВЫБОР ДВИГАТЕЛЕЙ

Произведем выбор двигателей, обеспечивая соотношение:

1) Для первого  канала выберем двигатель МИ-32 со следующими техническими данными:

 110В;

P= 0,37 кВт;

N=1000 об / мин (104,65 рад/с);

255 м;

4,2 A;

2,21Ом;

 

2) Для второго канала выберем двигатель МИ-32 со следующими техническими данными:

 110В;

P= 0,76 кВт;

N=2500 об / мин (261,6 рад/с);

255 м;

8,2 A;

0,391Oм;

 

3) Для третьего канала выберем двигатель МИ-21 со следующими техническими данными:

 110В;

P= 0,2 кВт;

N=2000 об / мин (209,3 рад/с);

153 м;

2,33 A;

2,2Oм;

 

В качестве модели двигателя воспользуемся упрощенной моделью (рис. 4):

 

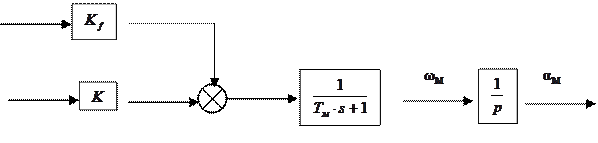Рисунок 4 - Упрощенная модель двигателя

; ;

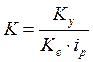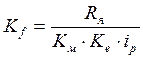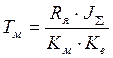
1)  Для первого канала:

i_p =100,

 ,  , , .

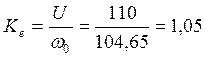
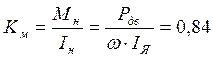
Суммарный момент инерции, приведенный к валу двигателя: 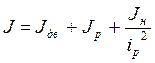, где  - момент инерции двигателя;

 - момент инерции редуктора;

 ;

=0,04 (c).

2)  Для второго канала:

i_p =80,

 ,  , , .

 ;

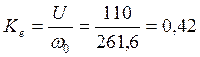
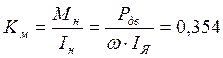
=0,043 (c).

3)  Для третьего канала:

i_p =60,

 ,  , , .

 ;

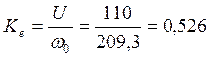
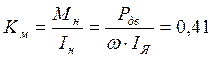
4)  =0,045 (c).

7 МОДЕЛИРОВАНИЕ

7.1 СИНТЕЗ АЛГОРИТМА СТАБИЛИЗАЦИИ

Стабилизация обеспечивается пропорциональным регулятором (алгоритмом управления) вида

,                                                                                           

где – матрица-строка коэффициентов обратной связи.

После подстановки алгоритма  получаем уравнение состояния замкнутой системы

, где . Соответствующий характеристический полином принимает вид

.

В соответствии с методом модального управления устойчивость положения равновесия синтезируемой системы и заданные динамические показатели качества  и  достигаются за счет назначения корней  характеристического уравнения , что в свою очередь обеспечивается соответствующим выбором коэффициентов обратных связей .

По заданным качественным показателям  с и  с использованием метода стандартных переходных функций найдем корни характеристического уравнения замкнутой системы  и коэффициенты желаемого характеристического уравнения . Выберем желаемую переходную характеристику, соответствующую биноминальному полиному второго порядка