Синтез робототехнической системы из трех вращательных кинематических пар пятого класса, страница 3

.

Нормированное время переходного процесса для   с, перерегулирование %. Минимально допустимый радиус распределения корней .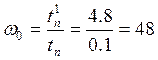

Возьмем

Коэффициенты полинома ,  и его корень

Коэффициенты матрицы обратной связи , соответствующей канонической (управляемой) форме объекта, рассчитываются как

.                                                                                         

.

Для обратного перехода (от канонической формы к исходному представлению системы) используется преобразование

,                                                                                

где – матрица преобразования (подобия), рассчитываемая как , а – матрица управляемости канонической модели ОУ.

, .

.

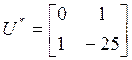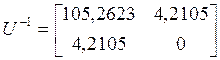1)

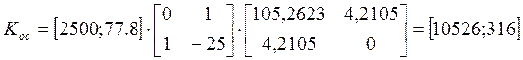
Для 2-ого и 3-его каналов алгоритм стабилизации аналогичен.

2)

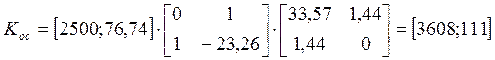
3)

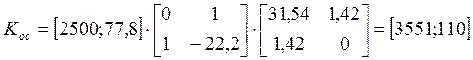
7.2 МОДЕЛИРОВАНИЕ ПЕРВОГО КАНАЛА

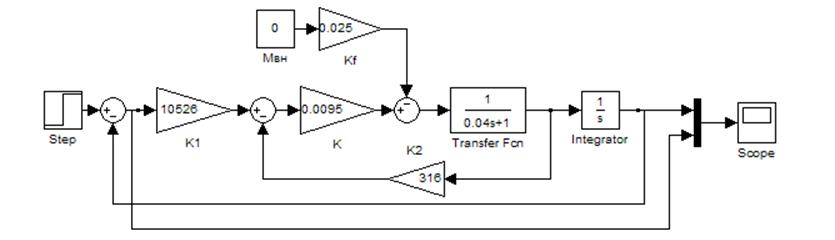
Рисунок 5 - Схема моделирования первого канала

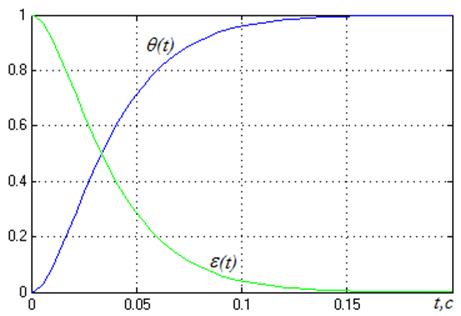
На рисунке 6 представлены результаты моделирования первого канала при единичном ступенчатом воздействии  и .

Рисунок 6

Ступенчатое воздействие система отрабатывает без ошибок.

Перерегулирование %;

Время переходного процесса =0.1 с.

На рисунке 7 представлены результаты моделирования первого канала при линейно нарастающем воздействи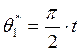и  и .

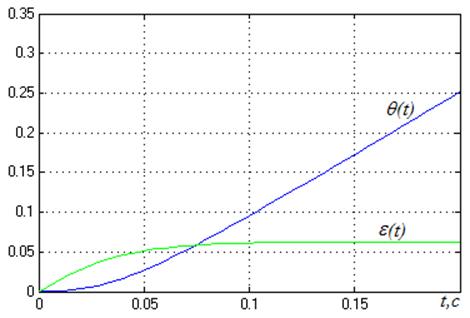
Рисунок 7

Линейно нарастающее воздействие система отрабатывает с постоянной ошибкой.

На рисунке 8 представлены результаты моделирования первого канала при воздействии с постоянным ускорением и .

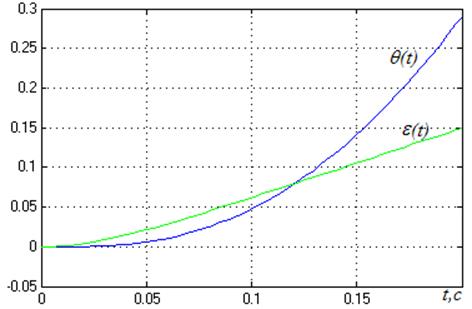
Рисунок 8

Воздействие  с постоянным ускорением система отрабатывает с линейно нарастающей ошибкой.

На рисунке 9 представлены результаты моделирования первого канала при единичном ступенчатом воздействии   и  .

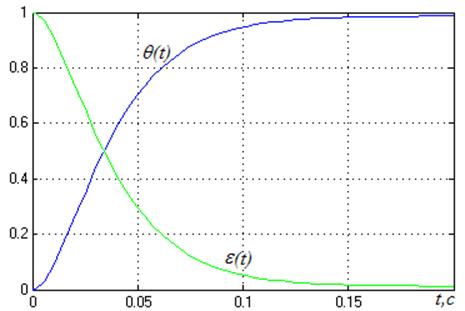
Рисунок 9

7.3 МОДЕЛИРОВАНИЕ ВТОРОГО КАНАЛА

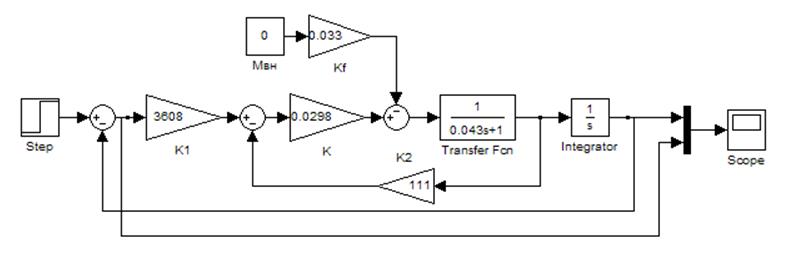
Рисунок 10 - Схема моделирования второго канала

На рисунке 11 представлены результаты моделирования второго канала при единичном ступенчатом воздействии  и .

Рисунок

11

Ступенчатое воздействие система отрабатывает без ошибок.

Перерегулирование %;

Время переходного процесса =0.1 с.

На рисунке 12 представлены результаты моделирования второго канала при линейно нарастающем воздействи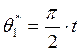и  и .

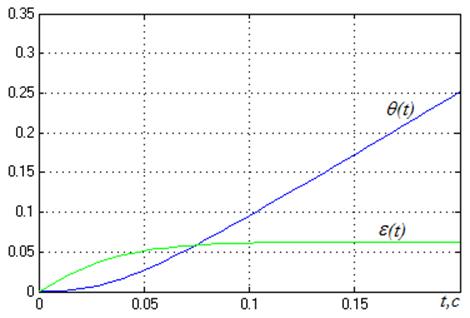
Рисунок 12

Линейно нарастающее воздействие система отрабатывает с постоянной ошибкой.

На рисунке 13 представлены результаты моделирования второго канала при воздействии с постоянным ускорением и .

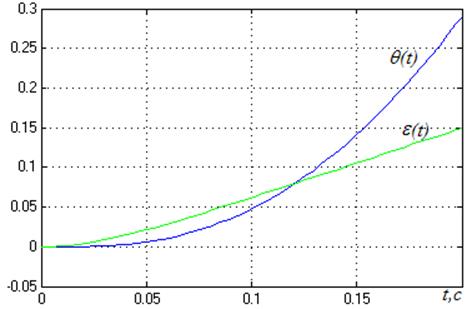
Рисунок 13

Воздействие  с постоянным ускорением система отрабатывает с линейно нарастающей ошибкой.

На рисунке 14 представлены результаты моделирования второго канала при единичном ступенчатом воздействии   и  .

Рисунок 14

7.4 МОДЕЛИРОВАНИЕ ТРЕТЬЕГО КАНАЛА

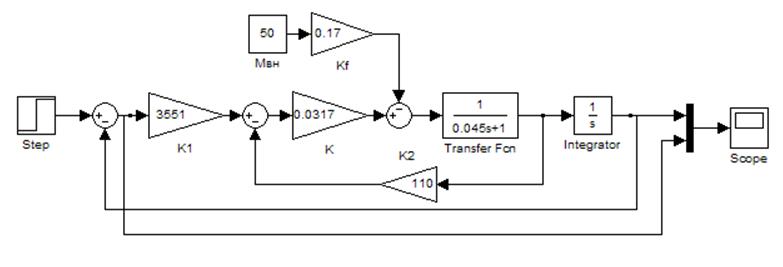
Рисунок 15 - Схема моделирования третьего канала

На рисунке 16 представлены результаты моделирования третьего канала при единичном ступенчатом воздействии  и .

Рисунок

16

Ступенчатое воздействие система отрабатывает без ошибок.

Перерегулирование %;

Время переходного процесса =0.1 с.

На рисунке 17 представлены результаты моделирования третьего канала при линейно нарастающем воздействи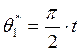и  и .

Рисунок 17

Линейно нарастающее воздействие система отрабатывает с постоянной ошибкой.

На рисунке 18 представлены результаты моделирования третьего канала при воздействии с постоянным ускорением и .

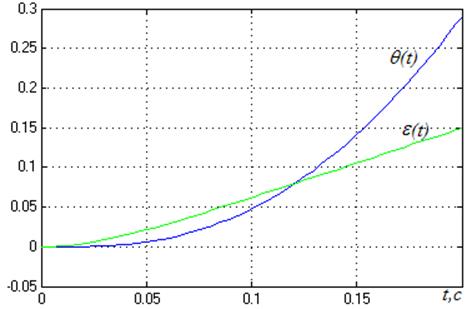
Рисунок 18

Воздействие  с постоянным ускорением система отрабатывает с линейно нарастающей ошибкой.

На рисунке 19 представлены результаты моделирования третьего канала при единичном ступенчатом воздействии   и  .

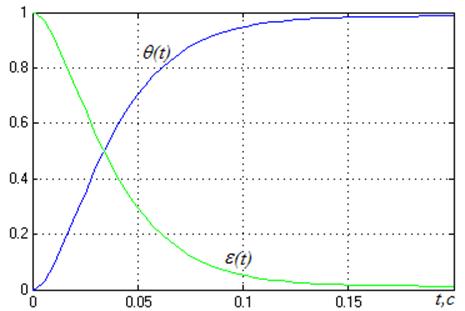
Рисунок 19

7.5 МОДЕЛИРОВАНИЕ ОБЩЕЙ СИСТЕМЫ

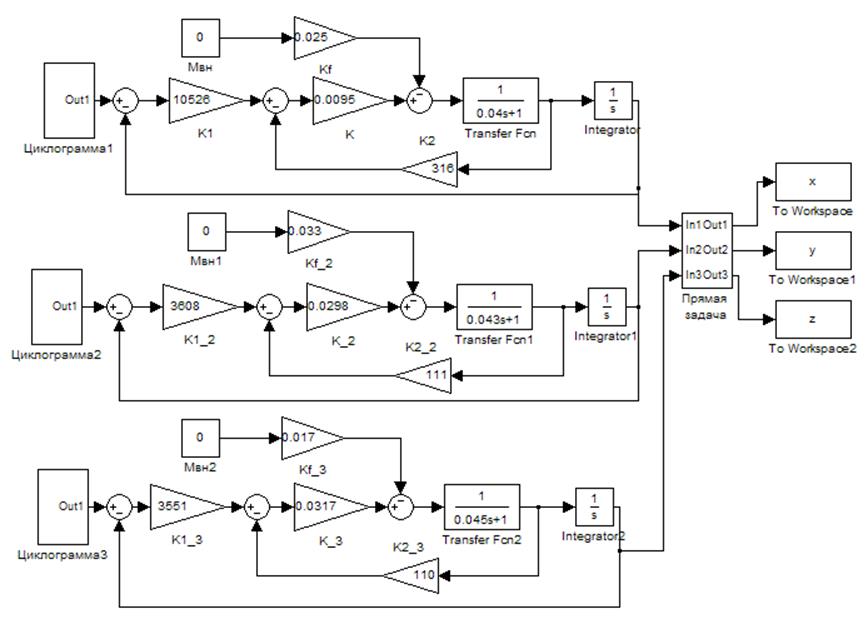
Рисунок 20 - Схема моделирования всей системы

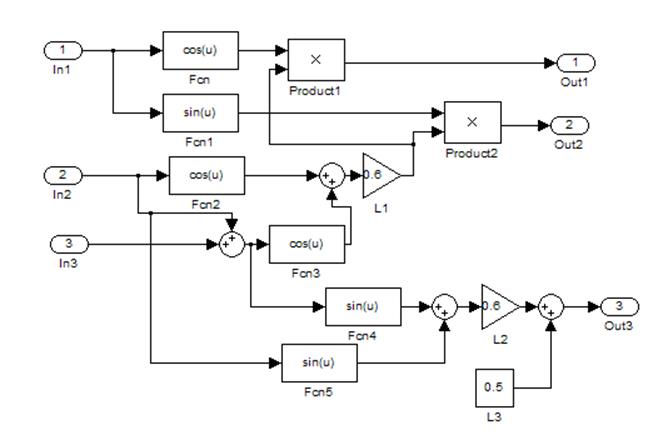
Рисунок 21 - Схема моделирования матрицы Rcx (решение прямой задачи)

Отработкациклограммы.

Зададим поведение робота следующим образом (см. таблицу 1):

Таблица 1

№ шага
1	0	0
2		0
3	0	0	0
4			0
5	0

Результаты моделирования по трем координатам представлены на рисунках 22 – 24 соответственно.

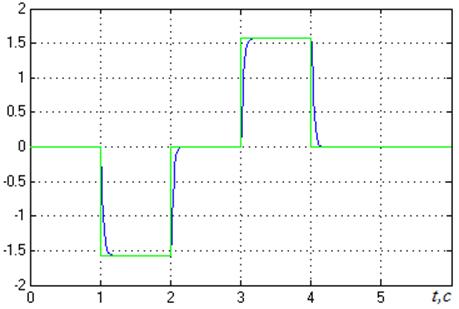
Рисунок 22 – Отработка циклограммы первым каналом

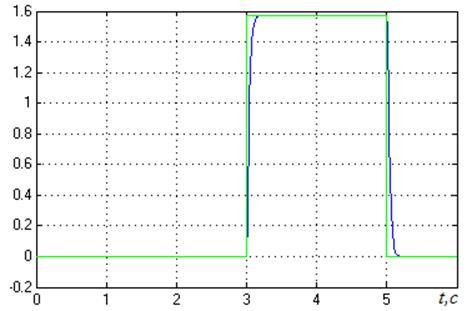
Рисунок 23 – Отработка циклограммы вторым каналом

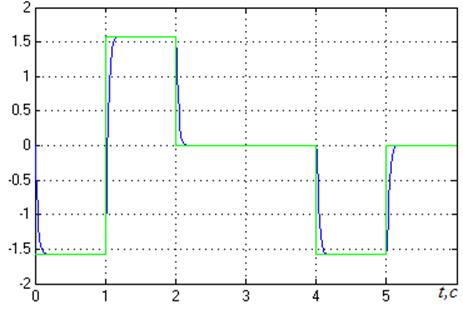
Рисунок 24 – Отработка циклограммы третьим каналом

На рисунке 25 представлена траектория движения манипулятора по трём координатам (x,y,z), в соответствии с пятью последовательными изменениями положения в пространстве этого манипулятора (в соответствии с циклограммой):

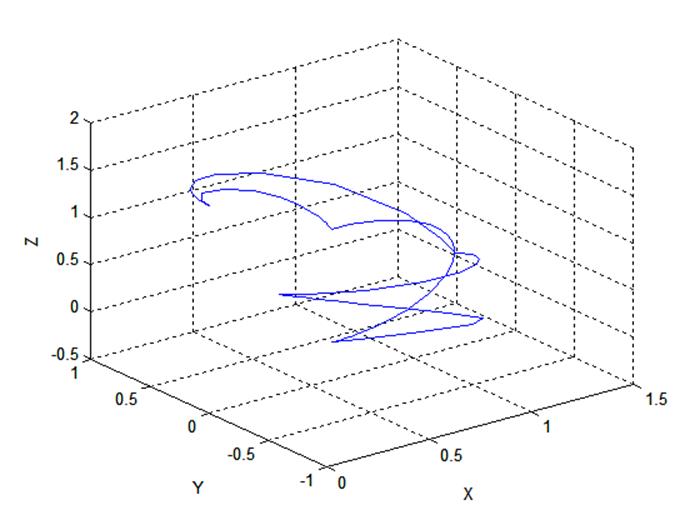
Рисунок 25 -  Траектория движения схвата манипулятора по заданной циклограмме