Пакет MatLab. Элементы программирования. Функции пакета. Графические возможности пакета, страница 12

subplot(m,n,p)

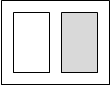
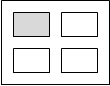
где m и n - количество строк и столбцов, p - номер области, в которую выводится первый график. Примеры использования команды subplot представлены ниже (заштрихованный прямоугольник показывает область в с которой начинается вывод графиков):

subplot(211)                     subplot(212)                     subplot(121)

 

subplot(122)                     subplot(221)                     subplot(111)

 

Пример:

t=0:pi/12:2*pi; [X,Y,Z]=cylinder(4*cos(t));

subplot(2,2,1); mesh(X)

subplot(2,2,2); mesh(Y)

subplot(2,2,3); mesh(Z)

subplot(2,2,4); mesh(X,Y,Z)

Команда mesh(Z)  создает график трехмерной перспективы элементов матрицы Z. Сетчатая поверхность определяется z координатами точек над прямоугольной сеткой в плоскости X-Y. При этом необходимо создать специальные матрицы X и Y, которые состоят из повторяющихся рядов и столбцов, соответственно, по всей области определения функции. Например (см. также функцию meshdom.m):

x=-8:.5:8;            y=x';

X=ones(y)*x;     Y=y*ones(x);

R=sqrt(X.^2+Y.^2)+eps);                             Z=sin(R)./R;

mesh(Z);

При построении поверхности можно установить точку просмотра. Для изменения точки просмотра трехмерной графики в данной версии пакета используется команда view, которая применяется после использования команды вывода поверхности:

mesh(z)

view[(az el])

Второй параметр - вектор V = [ az  el ] - содержит азимут горизонтального отклонения az (при вращении фигуры) и вертикальное отклонение el (при подъеме фигуры).

Сетка на графическом экране теперь может быть удалена после вывода графика (см. grid).

v=[0 17 0 10]; axis(v); s=1; xdm=10; cv='g'; ci='g';

for i=0:s:2*xdm

if i==1 title(' Пример '); end;

if i==xdm+1 s=-s; cv='r'; ci='b'; end;

if i<11 xd=i; else xd=2*xdm-i; end;

xn=2; yn=2; x=xd-s+xn+[0 0 1 3 3 3 0]; y=yn+[0 5 6 6 0 3 3]; plot(x,y,'i');

hold on, xn=7; yn=2; x=xn+[0 0 0 3 3]; y=yn+[0 3 0 3 0]; plot(x,y,'i');

xn=12; yn=2; x=-xd+s+xn+[0 3 1.5 1.5]; y=yn+[6 6 6 0]; plot(x,y,'i');

xn=2; yn=2; x=xd+xn+[0 0 1 3 3 3 0]; y=yn+[0 5 6 6 0 3 3]; plot(x,y,cv);

hold on, xn=7; yn=2; x=xn+[0 0 0 3 3]; y=yn+[0 3 0 3 0]; plot(x,y,ci);

xn=12; yn=2; x=-xd+xn+[0 3 1.5 1.5]; y=yn+[6 6 6 0]; plot(x,y,cv); pause(1);

end

§3. Графика пакета MatLabfor Windows.

Для вывода двухмерных графиков в данной версии пакета добавлены следующие функции:

bar                       - ступенчатый (столбцовый) график,

contour                - построение графика с контурными линиями (уровнями равных высот),

fill                         - график, заполненный цветом.

hist                       - гистограмма;

rose                      - угловая гистограмма;

stairs                    - построение графика в виде ступенчатой функции.

compass, errorbar, feather, fplot, quiver - см. help пакета MatLab.

Например:

t=0:.05:2*pi;

x=sin(t);              fill(x,t,’b’)

Команда оформления графиков - gtext(‘строка текста’), которая выводит текст на графике в место определенное положению мыши.

В пакете MatLab для Windows расширен список цветов графика. Добавлены цвета: y - желтый, m - сиреневый, c - голубой, k - черный. Исключен невидимый цвет - i, применение цветов c1,c2... не поддерживается.

Трехмерная графика в данной версии пакета представлена следующими функциями:

peaks                   функция генерации матрицы данных (параметр - количество точек для расчета поверхности, по умолчанию 49):

peaks

peaks(10)

plot3                    трехмерный график, представленный линиями и точками:

t=0:pi/50:10*pi;

plot3(sin(t),cos(t),t);

contour3             контурный график:

contour3(peaks,20)

pcolor                  прямоугольная область, цвета в которой определяются элементами матриц:

z=peaks; pcoor(z)

colormap(hot)

image                   вывод рисунка;

mesh, meshc, meshz         вывод поверхности:

x=-8:0.5:8; y=x;

[X,Y]=meshgrid(x,y);

R=sqrt(X.^2+Y.^2)+eps;

Z=sin( R )./R; mesh(Z)

surf, surfc, surfl               вывод поверхности:

colormap(cool); k=5; n=2^k-1;

theta=pi*[-n:2:n]/n;

phi=(pi/2)*[-n:2;n]’/n;

X=cos(phi)*cos(theta);