Achieving of parametric invariance by minimal control

ACHIEVING OF PARAMETRIC INVARIANCE BY MINIMAL CONTROL

Olga V. Slita

Department of Control Systems and Informatics

Saint-Petersburg State University of Information Technologies, Mechanics and Optics

Kronvercky av., 49, Saint-Petersburg, 197101, RUSSIA

Tel: (812) 595-41-28, E-mail: o-slita@yandex.ru

Abstract – conditions of achieving of absolute parametric invariance are formulated. A functional for finding of minimal control ensuring absolute parametric invariance is proposed.

1.  INTRODUCTION

In design of control systems desired quality coefficients are given by assigning a spectrum of desired eigenvalues. But when achieving parametric invariance there arises necessity of giving desired geometric properties of designed system by assigning a spectrum of desired eigenvectors. In cases when designer has a opportunity of choosing desired eigenvectors of many possible realizations, preferable choice is the one that is assigned by minimal control costs.

For such a case the given paper proposes a functional that helps evaluate control cost for assigning of desired eigenvectors and find vectors for which parametric invariance is achieved by minimal control.

2.  CONDITIONS OF ACHIEVING PARAMETRIC INVARIANCE

Consider the following linear continuous time plant

.                              (1)

where , , are state vector, control and output respectively;  are nominal component of state matrix, control and output matrixes: ;  is matrix variation of state matrix, ; besides matrix variation is such that pair  is controllable.

Let us design control law for plant (1) as an additive composition of external reference signal  forward control of with matrix  and state  feedback control with matrix  in assumption they are fully measured:

.                                                               (2)

Plant (1) and control law (2) make a system with the following vector-matrix representation:

;                                                   (3)

.                                                         (4)

In (3), (4)  is error between reference and output signals and matrixes  and  can be represented as

, ,                                                                        (5)

with matrix variation of state matrix of system satisfying equality

,                                                                    (6)

such that  is a Hurwitz matrix.

Invariance of the system output (and, hence, the error) regarding uncertainty  can be written in the following form

.                        (7)

Let us present matrix variation in additive form with minimal number of components so that the following condition holds

                                         (8)

By using representation (8) in (3) can be written in the following form:

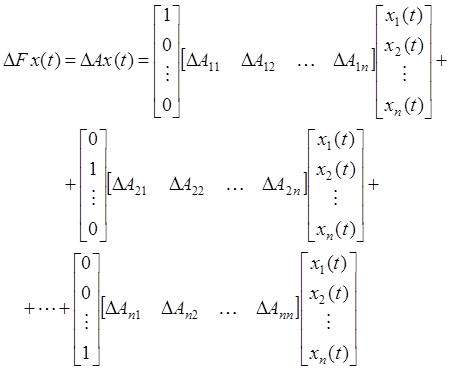                     (9)

In (9) first efficient of items (matrices-columns () dimension) are j-th columns  of matrix , so it is written in the form

.                                       (10)

Multiplicative vector structures

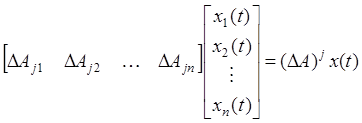,                       (11)

where  is –th row of matrix  are scalars and present components of vector of parametric influence , , where p in not more than n:

                                          (12)

Combination of (11) and (12) lets us present vector-matrix component  in the form:

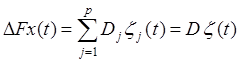.                                   (13)

Substitution of (13) into (3) lets us write:

.                   (14)

Problem of achieving of parametric invariance in the form (7) by using model (14) takes the view

.               (15)

In terms of Laplace transforms and transfer functions expression (15) takes the form

,                (16)

where  is Laplace image of reference signal ,  is Laplace image of “parametric” influence ,  is transfer function “reference signal – output of the system”,  is transfer function “parametric influence – output of the system”.

Obviously, this equality holds when

.                                               (17)

Let us formulate propositions, containing algebraic conditions of achieving of parametric invariance.

Proposition 1. For system (14) to be parametric invariant in the sense of condition (16), i.e. for transfer function (matrix) “parametric input  – system output ”  to be equal to zero, namely the following expression to hold

,         (18)

it is sufficient that

1)   – -th row of matrix  is eigenvector of the state matrix ;

2)   belongs to kernel of matrix  so that the following holds

.                                                                                                    (19)

Proof of proposition 2 can be found in [1].

Proposition 2. For column  of matrix  to be eigenvector of matrix  of the system (14) it is sufficient that vector  belongs to image of matrix , i.e. the following inclusion holds