Achieving of parametric invariance by minimal control, страница 2

.                                                                                     (20)

Proof of proposition 2 can be found in [2].

Algebraic condition (20) of belonging to image always holds if matrix B is of full rank, because its columns make basis.

So, it is possible to assign any desired structure of eigenvectors if rank of matrix B is equal to dimension of state vector of the plant. In this case problem of achieving of parametric invariance can be solved with feedback matrix K of the form

,                                            (21)

where , .

For such a case it is possible to assign desired structure of eigenvectors by substituting . Matrix is solution of system of matrix equations

,                                        (22)

,                                                    (23)

where equation (22) is Sylvester matrix equation [3,4].

3.  MAIN RESULT

As practice of control systems design shows, setting requirements of quality of transients and steady-state performance by assigning of desired structure of eigenvalues is of no difficulty. But it is more difficult to set requirements for desired structure of eigenvectors. If rank of matrix D is less than rank of matrix B than there appear freedom of assigning of eigenvectors structure with fixed eigenvectors ,  and non-fixed eigenvectors , , and hence, freedom in realization of matrix K and problem of evaluation of control cost and its distribution on sphere of initial conditions emerge. Let us use the following functional to evaluate control cost for assigning of every structure of desired eigenvectors and uniformity of its distribution

,                                          (24)

where  is grammian [5] of control cost, computed by virtue of Lyapunov-like equation

;                                             (25)

– maximal singular value [6] of grammian ;  is condition number of grammian .  determines maximal control cost, and  characterizes uniformity of distribution of these costs in sphere of initial conditions.

Let us illustrate choice of desired structure of eigenvectors with the following example.

4.  EXAMPLE

“Choice of desired eigenvectors, assigned by minimal control for 2^nd order plant with full-rank control matrix”

Consider 2^nd order plant, described by the following matrices 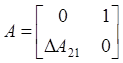, , 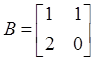, than matrix  takes the form .

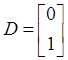Let us assign desired structure of eigenvalues of matrix  of closed-loop system as . First vector of eigenvectors structure is , and the second one is given in parameterized form 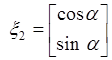, where  is angle of rotation of  around point of origin.

Matrix  takes diagonal form 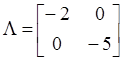 and matrix of similarity of matrices  and , which contains eigenvectors, is .

Let us solve Sylvester matrix equation relatively to matrix  and compute feedback matrix  with equation (23)

,

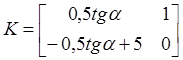and find values of angle  for which functional (24) takes minimal and maximum values.

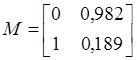Figure 1 shows dependence of maximal singular value and condition number on value of angle . Dependencies on the figure show, that functional (24) takes minimal value at angle . Thus we conclude that matrix  should be chosen as  to ensure the least control cost.

Figure 1. Dependence of maximal singular value  and condition number  on value of angle .

5. CONCLUSION

In the given work a functional which helps finding of minimal control cost while assigning parametric invariance is proposed. Results are illustrated by an example.

6.  ACKNOLEGEMENT

The author is grateful to Department of Control Systems and Informatics of SPb SUITMO for favourable research atmosphere and A. V. Ushakov for helpful discussing and approval of results presented in the paper.

7.  REFERENCES

[1] Slita O. V., Ushakov A. V., Model Representation of the Control Object in the Task of Parametric Invariance. // Proceedings of institutes of higher education. Priborostroeniye. 2006. V. 49. № 1. pp.14–20. (In Russian).

[2] Slita O. V., Ushakov A. V., Rank Factor of Control Matrix of a Dynamical Plant in Problem of Achieving Parametrical Invariance.// Modern Technologies: Collected articles/ edited by S.A. Kozlov., SPb SITFMO (TU), 2003. pp.253–259. (In Russian).

[3] Nikiforov V.O., Ushakov A.V. Control in uncertain conditions: sensitiveness, adaptation, robustness.  Saint-Petersburg: SPb SITFMO (TU), 2002. (In Russian).

[4] Ushakov A.V. Generalized modal control. // Proceedings of institutes of higher education. Priborostroeniye. 2000. V. 43. № 3. pp.8–16. (In Russian).

[5] Mironovsky L. A. Functional Diagnostics of Dynamic Systems. M – SPb.: MSU – GRIF Publishers, 1998.

[6] G. H. Golub and C. F. Van Loan, Matrix conputations/ M.: Mir, 1999. (in Russian).