present input-output model (6) as input-state-output model
![]()
![]() ,
, ![]() , (7)
, (7)
where ![]() is state of model (7),
is state of model (7), ![]() ,
, ![]() ,
, ![]() и
и ![]() are transformation matrices from input-output model
(6) to input-state-output model (7). As polynomial
are transformation matrices from input-output model
(6) to input-state-output model (7). As polynomial ![]() is Hurwitz and model (6) is strictly minimum phase,
according to consequence 3 [4], it is possible to determine a symmetric
positively determined matrix
is Hurwitz and model (6) is strictly minimum phase,
according to consequence 3 [4], it is possible to determine a symmetric
positively determined matrix ![]() , satisfying two following matrix equations:
, satisfying two following matrix equations:
![]() ,
, ![]() ,
(8)
,
(8)
where ![]() , entries of matrix
, entries of matrix ![]() depend on parameter
depend on parameter ![]() and do not depend on parameter
and do not depend on parameter ![]() .
.
Consider derivative of function of
deviation ![]()
![]() ,
(9)
,
(9)
where ![]() .
.
Let us present a theorem describing
conditions for calculation of parameter ![]() and function
and function ![]() , ensuring accomplishing of purpose of control.
, ensuring accomplishing of purpose of control.
Theorem. There exist a parameter ![]() and a function
and a function ![]() such as all trajectories of system (7), (9) can be localized in any
small area by increasing of parameter
such as all trajectories of system (7), (9) can be localized in any
small area by increasing of parameter ![]() .
.
Proof. Consider a Lyapunov function of the form
![]() , (10)
, (10)
where
![]() ,
(11)
,
(11)
![]() .
(12)
.
(12)
Differentiating (11) with respect to time subject to equation (7) we obtain
![]()
![]()
![]() ,
(13)
,
(13)
Substituting equations (8) into (13) and considering the following equations
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
for derivative of Lyapunov function (11) we obtain
![]() , (14)
, (14)
where small value ![]() .
.
Differentiating (12) with respect to time subject to equation (7) we receive
![]()
![]() (15)
(15)
where in equation (15) ![]() was substituted by summand
was substituted by summand
![]()
Then, considering inequalities
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
for derivative of function (12) we obtain
![]()
![]()
![]() (16)
(16)
for derivative of Lyapunov function (10) we obtain
![]()
![]()
![]() .
(17)
.
(17)
Let us choose ![]() such a way that the following inequality holds
such a way that the following inequality holds
![]() ,
(18)
,
(18)
where ![]() is a positively determined matrix.
is a positively determined matrix.
Choose function ![]() , so the following inequality holds
, so the following inequality holds
![]()
![]() ,
(19)
,
(19)
where ![]() .
.
Then, according to restrictions on the nonlinearity for derivative of Lyapunov function (10) we obtain
![]() (20)
(20)
Choosing number ![]() as
as
![]() ,
(21)
,
(21)
we obtain
![]() .
(22)
.
(22)
From inequality (22) as disturbance ![]() is bounded, it follows that there exists
such
is bounded, it follows that there exists
such ![]() , that trajectories of system (7), (9) can
be localized in any given area
, that trajectories of system (7), (9) can
be localized in any given area![]() , which was to be proved.
, which was to be proved.
Consider results of computer simulation of
Van der Pole system. First let us assume that ![]() and there appear stable oscillations in system (1) (system possesses
a stable limit cycle). Then, with harmonic disturbance there arise chaotic
phenomena in the system. And finally, on the last step of simulation of system
(1) with control law (3), (4), we discover accomplishment of purpose of
control.
and there appear stable oscillations in system (1) (system possesses
a stable limit cycle). Then, with harmonic disturbance there arise chaotic
phenomena in the system. And finally, on the last step of simulation of system
(1) with control law (3), (4), we discover accomplishment of purpose of
control.
Figures 1 and 2 show results of computer
simulation of undisturbed system (1) for ![]() ,
, ![]() ,
, ![]() (Figure 1) and disturbed system (1) for
(Figure 1) and disturbed system (1) for ![]() ,
, ![]() ,
,![]() (Figure 2) respectively. Results of
computer simulations (Figures 1 and 2) show, that system (1) possesses stable
limit cycle in absence of disturbance (
(Figure 2) respectively. Results of
computer simulations (Figures 1 and 2) show, that system (1) possesses stable
limit cycle in absence of disturbance (![]() ) and that in presence of harmonic disturbance (
) and that in presence of harmonic disturbance (![]() ) there appear chaotic processes in system
(1).
) there appear chaotic processes in system
(1).
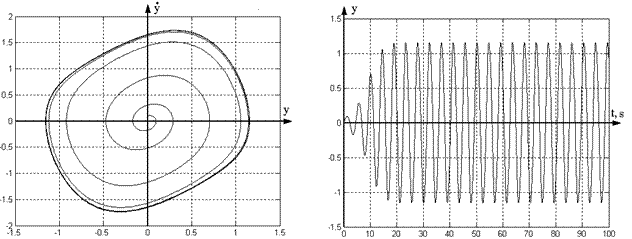 |
Fig. 1. Phase portrait and transients of
system (1) for ![]() ,
, ![]() .
.
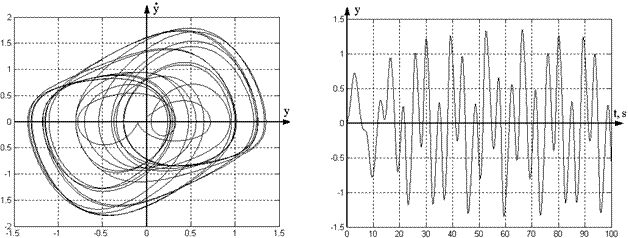 |
Fig. 2. Phase portrait and transients of
system (1) for ![]() ,
, ![]() .
.
To stabilize system (1) let us choose
control algorithm (3). Choose polynomial ![]() , then
, then
![]() ,
(23)
,
(23)
where function ![]() is formed by estimation algorithm (4).
is formed by estimation algorithm (4).
Function ![]() is chosen so that inequality (19) holds, i.e.
is chosen so that inequality (19) holds, i.e.
![]() .
(24)
.
(24)
Let us choose parameter ![]() , and simulate control system for different values of
parameter
, and simulate control system for different values of
parameter ![]() . Transients of closed loop system for
nonzero initial conditions (
. Transients of closed loop system for
nonzero initial conditions (![]() ) and values
) and values ![]() and
and ![]() are shown on Figure 3.
are shown on Figure 3.
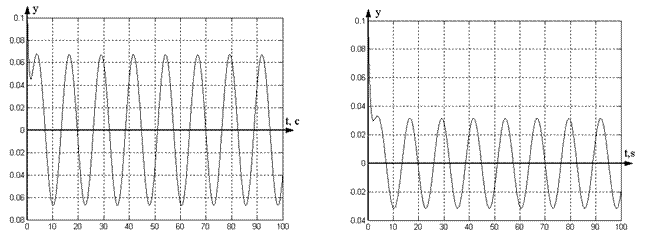 |
Fig. 3. Transients of system (1), (23),
(24) for ![]() and
and ![]() ,
, ![]() .
.
4. Conclusion
An algorithm of output control of a nonlinear chaotic system, described by Van der Pole equality is proposed. The proposed control law ensures convergence of output trajectory of the nonlinear system to an area, and this area can be reduced by increasing of controller parameter.
5. References
[1] B.R. Andrievskii, A. L. Fradkov, “Control of Chaos: Methods and Applications. I. Methods”, Automation and Remote Control, vol. 64, no. 5, 2003, pp. 673-713.
[2] B.R. Andrievskii, A.L. Fradkov, “Control of Chaos: Methods and Applications. II. Applications”, Automation and Remote Control, vol. 65, no. 4, 2004, pp. 505-533.
[3] T. Gilbert and R.V. Gammon, “Stable oscillations and devil’s staircase in the Van de Pole oscillator”, International Journal of bifurcation and chaos, vol. 20, no. 1, 2000, pp. 155-164.
[4] A.A. Bobtsov and N.A. Nikolaev, “Fradkov theorem-based design of the control of nonlinear systems with functional and parametric uncertainties”, Automation and remote control, vol. 66, no. 1, 2005, pp. 108–118.
[1] This work was supported by grant of Federal Agency of Sciences
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.