Identification of unknown noise statistics for non-stationary state space systems

IDENTIFICATION OF UNKNOWN NOISE STATISTICS FOR NON-STATIONARY STATE SPACE SYSTEMS

Tanya V. Podladchikova

Institute for applied system analysis at National technical university of Ukraine “Kyiv Polytechnical Institute”, av. Pobedy 37, Kiev, 03056, UKRAINE, E-mail: tpodlad@rambler.ru

Abstract — Pseudo-measurements creation of unknown noise covariances and expectation lets us to propose such algorithmic structure, which can be used for the identification of noise statistics in the conditions of variable parameters of state space model, namely time-varying state-transition matrix and time-varying input matrix. Simplicity of the proposed method and small computation time make it useful for its application in real time scale.

1. INTRODUCTION

Many industrial processes can be described by linear, discrete time state space models. The state space models are used for the problems solution of control, diagnostics, pattern recognition in communications, energetics, machine building, aviation, chemical industry, physics, geology, economics and biology.

Making precise state estimation is inseparable from stochastic effect, which can enter in one of two ways:  either being intrinsic to the process itself or as a consequence of measurement error. In order to use the optimal filter, we need to know the expectations and covariances of the disturbances. However, in the most industrial applications the statistical characteristics of the disturbances entering the process are not known.

A great number of approaches were proposed for the identification problem of noise statistics, which can be divided into four general categories: Bayesian [1, 2], maximum likelihood [3, 4], covariance matching [5], correlation techniques [6-9]. Nevertheless, Bayesian and maximum likelihood methods require an excessive computation time, which limits their practical applications.

Most of identification methods are confined to stationary models. The assumption of stationarity is great convenience because it means that statistical characteristics of model noises can be estimated by time averaging.

Some authors have reported about simple computation algorithms of consistent estimations of noise statistics on the basis of time averaging of m-dependent sequences formed by measurements. In particular, Anderson [10] proposed to estimate the noise covariances by means of creation of 1 and 2-dependent sequences. One more approach is based on creation of residuals of suboptimal filter with fixed memory [11]. This filter is built for the dynamical system that is free from state noise. Therefore the estimations of expectations and covariances were determined by means of creation of n and (n+1)-dependent sequences of residuals or residuals products (n is dimension of state vector).

These approaches are potential useful for identification in conditions of variable parameters of state space model.

The aim of this paper is to transform the indicated algorithms to the non-stationary models with time-varying state-transition matrix and time-varying input matrix.

The section 2 contains a transformation description of approach taken by Anderson to the non-stationary systems. In section 3 the extension of method based on creation of filter residuals with fixed memory is described for non-stationary one-dimensional model in order to demonstrate clearly its essence.

2. CREATION OF PSEUDO-MEASUREMENTS OF ESTIMATING NOISE COVARIANCES

Mathematically, linear state space model is described by the following set of difference equations:

                                                                                                                                              (1)

                                                                                                                                               (2)

in which , , ,  and  are uncorrelated zero-mean Gaussian noise sequences with covariances  and .

Identification method proposed by Anderson in the conditions of observability of all components of state vector () is applicable for time-invariant matrixes , . To estimate the noise covariances, when these matrixes are time-varying, the following sequences based on measurements are created:

.                                                                          (3)

The expectations of  are given by

,                                                                                          (4)

.

Pseudo-measurements of covariances  are determined in the following way:

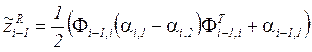.                                                                                               (5)

.

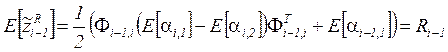So,  can be considered as sequence of pseudo-measurements of matrix  in the presence of additive noise. As this noise is 2-dependent zero-mean sequence and all parameters of model are bounded, then the consistent estimate of time-invariant covariance  can be determined in the following way

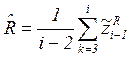.                                                                                                                                          (6)

Let us denote by  the pseudo-measurements of covariances . According to (4) the elements of  are determined from the linear system of equations