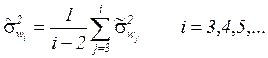 ,
(11)
,
(11)
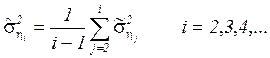 . (12)
. (12)
The expressions (9 –12) determine the consistent estimations of time-invariant noise variances in conditions of unequally-spaced observations when time intervals between measurements are bounded.
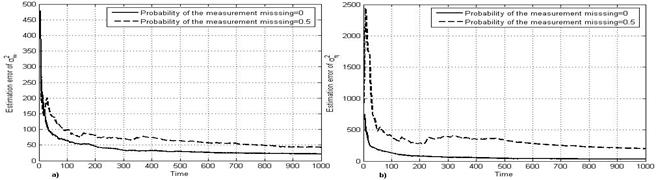
The Figure 1 depicts the behavior of mean
square errors of estimations ![]() (Figure 1a) and
(Figure 1a) and
![]() (Figure 1b) obtained on the basis of statistical
modeling.
(Figure 1b) obtained on the basis of statistical
modeling.
Figure
2. The behavior of mean square errors of estimations: a)![]() ; b)
; b) ![]() .
True values
.
True values ![]() ;
; ![]() .
Solid curve:
.
Solid curve: ![]() , probability of
measurement omission
, probability of
measurement omission ![]() ; dash curve:
; dash curve: ![]() ,
, ![]() .
.
As Figure shows, the accuracy of estimation is high despite the fact that half of measurements were missed.
The expressions (11), (12) use every new pseudo-measurement
![]() and
and ![]() as equivalent additional information
to already available information. When the variances
as equivalent additional information
to already available information. When the variances ![]() and
and ![]() are time-varying, the current pseudo-measurements
are more important than previous, so the previous measurements have to be used
with smaller weight. Therefore, the method of exponential smoothing with smoothing
constants
are time-varying, the current pseudo-measurements
are more important than previous, so the previous measurements have to be used
with smaller weight. Therefore, the method of exponential smoothing with smoothing
constants ![]() and
and ![]() can be used for the identification of
time-varying noise variances in conditions of unequally-spaced observations.
can be used for the identification of
time-varying noise variances in conditions of unequally-spaced observations.
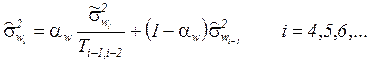 ,
(13)
,
(13)
![]() (14)
(14)
To increase the prediction accuracy of
non-stationary processes, it is rational to suppose about existence of non-zero
expectation ![]() of noise
of noise ![]() and to build adaptive Kalman filter on the
basis of identification of both the noise variances and expectation.
and to build adaptive Kalman filter on the
basis of identification of both the noise variances and expectation.
The following 1-depentent sequence can be
considered as pseudo-measurements of noise expectation ![]() in conditions of unequally-spaced
observations
in conditions of unequally-spaced
observations
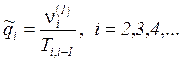 (13)
(13)
The consistent estimate of time-invariant expectation
is giving by 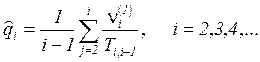 .
.
Time-varying expectation in conditions of unequally-spaced observations is defined in the following way
![]() ,
(14)
,
(14)
in which ![]() - smoothing constant.
- smoothing constant.
In conditions of non-zero expectation of
noise ![]() in the expressions (9) and (10)
instead of residuals
in the expressions (9) and (10)
instead of residuals ![]() and
and ![]() centralized
values
centralized
values 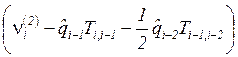 and
and ![]() are used.
are used.
So, the identification algorithm in conditions of unequally-spaced observations includes next steps:
1.
Identification of expectation
![]() in accordance with expressions (13), (14).
in accordance with expressions (13), (14).
2.
Identification of variance
![]() in accordance with expression (9), (13).
in accordance with expression (9), (13).
3.
Estimation of variance ![]() in accordance with expression (14).
in accordance with expression (14).
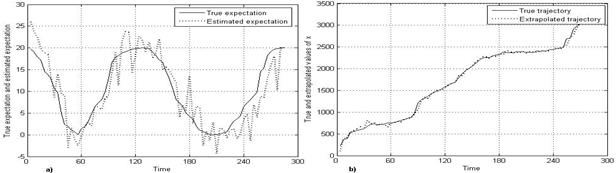
To estimate effectiveness of proposed
algorithm, the modeling of adaptive Kalman filter for non-stationary trajectory
of random walk was performed. The Figure 2a shows the modeling behavior of true
expectation of noise ![]() (solid curve) and its
estimation in conditions of measurements omission (dotted curve). The Figure 2b
depicts the modeling trajectory of random walk and its extrapolated values for
one step on the basis of the identification of noise statistics
(solid curve) and its
estimation in conditions of measurements omission (dotted curve). The Figure 2b
depicts the modeling trajectory of random walk and its extrapolated values for
one step on the basis of the identification of noise statistics ![]() ,
, ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.