Identification of unknown noise statistics for non-stationary state space systems, страница 2

.                                                                                                     (7)

The consistent estimate of time-invariant matrix  is given by

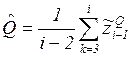.                                                                                                                                          (8)

So, the expressions (3), (5-8) determine the identification algorithm of noise covariances  and  in conditions of time-varying state-transition matrix and time-varying input matrix.

To estimate the accuracy and convergence rate of the proposed algorithm, statistical modeling was used for the non-stationary model with determinate polynomial base disturbed by zero-mean uncorrelated random acceleration with unknown variance . Coordinate  and its rate are the components of the state vector  for the model (1). The state-transition matrix 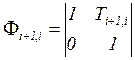; input matrix .

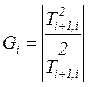It is supposed that the coordinate x and its rate are measured in presence of additive uncorrelated zero-mean noise  with unknown covariance 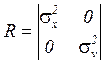. Then matrix in the equation (2) is unitary matrix. It is supposed also that time interval between measurements is variable because of possible measurements omission, which probability is determined by. So the matrixes  and  are time-varying.

The Figure 1 depicts the behavior of mean square errors of estimations, and  obtained on the basis of statistical averaging of 100 realizations of trajectory. The minimal time interval between measurements  can increase in accordance with number of missed measurements (). The true values of estimating variances ,,. As figure shows, the accuracy of estimation of unknown variances increases during the all observation period . Errors of estimation of  (Figure 1.a, solid curve) are approximately three times greater than those of (Figure 1a, dash curve). A priory information about covariance  lets us to increase the accuracy of estimation of  (Figure 1b, dash curve) 

Figure 1. The behavior of mean square errors of estimations: a) , ; b).

in comparison with this estimation in conditions of unknown covariance  (Figure 1.b, solid curve).

3. IDENTIFICATION OF NOISE STATISTICS ON THE BASIS OF FILTER RESIDUALS

Let us consider the non-stationary one-dimensional model of random walk described by the following set of difference equations

in which  and  are uncorrelated zero-mean noise sequences with unknown variances  and .

Let us create the 2 and 1-dependent sequence of pseudo-measurements  и  of variances  and  in conditions when . Filtered estimate of state  on the basis of filter with memory 1 and extrapolated one for next step are giving by . The filter residual .  The state estimation of  built for the model of free dynamical system on the basis of filter with memory 2 is giving by 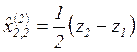, and corresponding residual is determined by 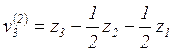. For every  let us determine analogically the 2-depentent sequence of residuals product  on the basis of filter with fixed memory 1 and 2.

As  and , then

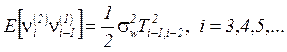. So, the expression

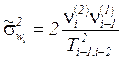                                                                                                                                            (9)

can be considered as pseudo-measurements of variance .

As , then the pseudo-measurements of  are giving by

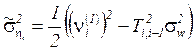                                                                                                                        (10)

The estimations of time-invariant variances