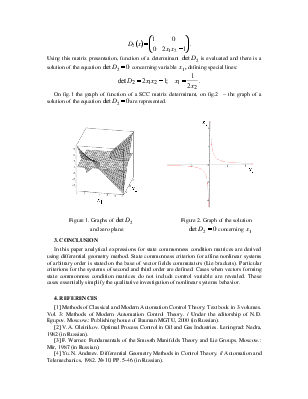
Analysis of state commonness condition of nonlinear systems with differential geometry methods

ANALYSIS OF STATE COMMONNESS CONDITION OF NONLINEAR SYSTEMS WITH DIFFERENTIAL GEOMETRY METHODS

Alexander V. Baranov

Department of Automation and Control Processes

Saint-Petersburg State University of Electrical Engineering

Prof. Popov str. 5, Saint-Petersburg, RUSSIA

Tel: +7(812) 2343798, E-mail: loge@yandex.ru

     Abstract – Analytical expressions for state commonness condition matrices are derived using vector fields commutators (Lie brackets). State commonness criterion for affine nonlinear systems of arbitrary order is stated on the base of differential geometry method. Cases when vectors forming state commonness condition matrices get out of control are revealed. These cases essentially simplify the qualitative investigation of nonlinear systems behavior.

     1. INTRODUCTION

     Controllability and state commonness (SC) problems of nonlinear control systems are fundamental and nowadays don’t have their final solution. The solution is possible only for the objects of certain class and in fixed functioning conditions. Solution complexity noticeably increase with the rise of model order. The success of nonlinear systems with complicated structure synthesis is based on the ability to solve the problem of principle control capability of the given object. Ignoring of this question during system design process can lead to serious consequences when operating real technical objects.

     Present-day state of control theory and practice admits different approach to mentioned problems decision. Use of linear algebra apparatus for nonlinear systems often proves to be insufficient and inadequate. From this emerges the need for the use of differential geometry methods and different algebras (Lie algebras in particular) [1]. Geometrical approach gives possibility to look thoroughly at many fundamental problems of control theory, including state commonness problem. Notion of state commonness condition (SCC) in the form of vector field commutators allows to determine the similarity and differences in the controllability and state commonness criterion for the prototype systems of various order. Stated criterion presentation also allows to reveal new qualitative properties of control objects behavior.

     Mathematic model of control object. We consider the affine (linear by control) system (object) described by the following differential equation system:

                                                               ,                                               (1)

where  – -dimension vector; ,  – nonlinear vector-functions;  – scalar control variable.

     Problem definition. The problem of getting a SCC matrix and criterion for the various order objects in the form (1) using differential geometry method, Lie brackets and vector field properties is set. In particular objects of second and third order and their behavior are subject to detailed analysis.

     2. MAIN RESULTS

     2.1. State commonness criterion for arbitrary order control objects

     According to [2] SCC of  nonlinear object of  kind (1) is established on the basis of using a block matrix

                                             ,                             (2)

where functional elements  are by means of the following recurrent parities:

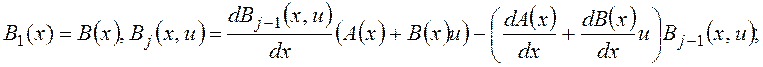
.   (3)

Matrix   is called SCC matrix for the nonlinear control objects in the form (1).

     It is necessary to notice that model (1) is a special case of the description used in (2), therefore all conclusions and parities received in (2) for objects with vector control appear correct for the objects with scalar control. SC criterion is fulfillment of a condition

,

i.e. SCC matrix should be a matrix of a full rank for any moment of time. At  there are special cases corresponding to reduction of state space dimension.

     If to enter a designation , expression (3) can be transformed to a kind:

.                                                                               (4)

     As is known [3], commutator of two vector fields (Lie brackets) of the first order has the following presentation:

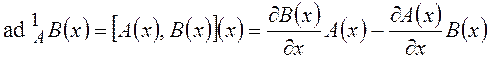                               .               (5)

The commutator (5) puts in correspondence to vector fields  и  new vector field, where  represents a Jacobi matrix of the vector field.

     Using vector field commutator (5), expression (4) can be represented as:

                           .           (6)

As a result the recursion formula for an evaluation of component vectors of SCC matrix  with use of Lie commutators of the first order is gained.

     Applying formula (6), expression (2) is reduced in an aspect:

(7)

Deriving notion (7), it has been taken into account that

                                               .                               (8)

     Block matrix (7), in which Lie brackets of the zero and first order are defined by expressions (8) и (5) accordingly, represents SCC matrix for nonlinear systems of an aspect (1). SC criterion for the introduced presentation of SCC matrix is realization of a requirement:

                                                          ()                                         (9)

for any instant.

     In [2] it was noted that presence of control in expressions for the elements of functional matrix complicates controllability and SCC analysis in nonlinear case. Actually, according to (6) every vector  in SCC matrix, except the first one , depends on control variable . However the obtained recursion introducing (6) allows to formulate requirements when control variable will not participate in vectors, component SCC matrix, defined (7). For this it is necessary that the item in the right part of the expression (6) was equal to zero. Supposing control variable nonzero (), the given requirement will be fulfilled securing of equality

                                                              .                                            (10)