In turn realization of
(10) is possible, if in a point where the commutator is evaluated, directions of
vector fields ![]() и
и ![]() coincide. Thus two vector fields will
commute, and their commutator is identically equal to zero [4]. If the given requirement
will be fulfilled for every
coincide. Thus two vector fields will
commute, and their commutator is identically equal to zero [4]. If the given requirement
will be fulfilled for every ![]() ,
, ![]() in relation to a vector
in relation to a vector ![]() describing
initial object, SCC matrix (7)can be represented as:
describing
initial object, SCC matrix (7)can be represented as:
![]() . (11)
. (11)
SC criterion for this introduction also is the rank criterion (9) for any instant.
On the basis of the suggested approach now it is possible to review nonlinear objects of the second and third order having the specific singularities of introduced SCC matrices.
2.2. State commonness criterion for control objects of the second order
SCC matrix for objects of the second order is represented according to (2) as follows:
![]() ,
,
where
 . (12)
. (12)
Using a recurrent formula
(3) for ![]() using Lie commutators, it is possible to
note:
using Lie commutators, it is possible to
note:
![]() . (13)
. (13)
Taking into account that ![]() and also the property
stating that result of two equal vector fields commutation is equal to zero [4],
expression (13) will become:
and also the property
stating that result of two equal vector fields commutation is equal to zero [4],
expression (13) will become:
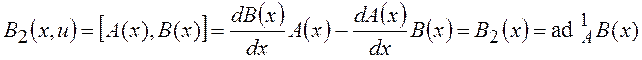 . (14)
. (14)
From (14) it is clear that vector ![]() does not depend on
control variable
does not depend on
control variable ![]() and accuracy is equal to the commutator of
the first order concerning vector fields
and accuracy is equal to the commutator of
the first order concerning vector fields ![]() и
и ![]() , i.e. initial vectors of object under
consideration. Thus, for objects of the second order the SCC matrix in view of
above-stated will be noted as follows:
, i.e. initial vectors of object under
consideration. Thus, for objects of the second order the SCC matrix in view of
above-stated will be noted as follows:
![]() . (15)
. (15)
State commonness
criterion for
considered objects will be realization of a requirement ![]() (
(![]() ) for any instant.
) for any instant.
The obtained expression (15)
allows to
make the following conclusions. Elements of block SCC matrix for the objects of
the second order and, accordingly, its determinant do not depend on the control
attached to the object. This, in turn, specifies that cases when coordinates of
object during its movement do not fulfill to state commonness criterion (so
called losses of state commonness) depend exclusively on natural properties of
object and follows from the equations describing it. It is possible to judge a
linear dependence of columns and rows of SCC matrices on its rank. In the given
case rank definition of ![]() matrix is not complicated because control
variable
matrix is not complicated because control
variable ![]() is not present in the evaluation formulas. Thus,
the qualitative analysis of system movements is not at a loss. Therefore, at SCC
definition for introduced control objects of the second order it is not
necessary to know the law of change of
is not present in the evaluation formulas. Thus,
the qualitative analysis of system movements is not at a loss. Therefore, at SCC
definition for introduced control objects of the second order it is not
necessary to know the law of change of ![]() and make supposition concerning
what class o functions it belongs to. When solving a problem of optimal control
on speed it is supposed that control variable should belong to a class of piecewise
functions. It is important to note that for the objects of the second order SC criterion
coincides with the controllability conditions suggested in [5].
and make supposition concerning
what class o functions it belongs to. When solving a problem of optimal control
on speed it is supposed that control variable should belong to a class of piecewise
functions. It is important to note that for the objects of the second order SC criterion
coincides with the controllability conditions suggested in [5].
2.3. State commonness criterion for control objects of the third order
In this paragraph we briefly review the main results obtained for affine nonlinear systems of the third order. State commonness matrix for the above mentioned objects in terms of Lie algebra becomes:
![]() , (16)
, (16)
where Lie commutators of the second order are defined as follows:
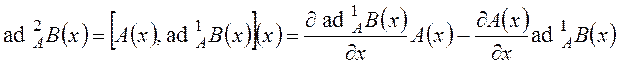 . (17)
. (17)
If ![]() (case when vector fields
(case when vector fields ![]() and
and ![]() commutate) expression (16) can be
written:
commutate) expression (16) can be
written:
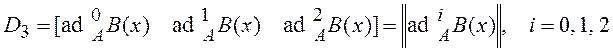 . (18)
. (18)
State commonness
criterion for systems of the third order will be requirement ![]() (
(![]() ) for
any moment of time.
) for
any moment of time.
2.4. Example. For control system
![]()
it is required to carry
out SC analysis. Such mathematical models are widely applied to exposition of
dynamical objects and processes in different fields of industry [2]. With the purpose
of simplification we assume![]() , that does not influence on generality of analysis.
Vector functions of the accepted object description look as follows:
, that does not influence on generality of analysis.
Vector functions of the accepted object description look as follows:
 .
.
Functional vectors of SCC matrix are defined, according to (3), (14), as:
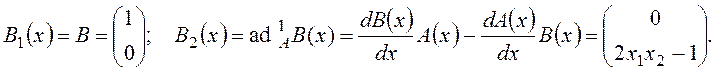
Block SCC matrix (15) composed from the obtained vectors, has the following notation:
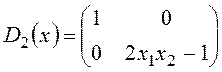 .
.
Using this matrix presentation,
function of a determinant ![]() is evaluated and there is a solution of the equation
is evaluated and there is a solution of the equation ![]() concerning
variable
concerning
variable ![]() , defining special lines:
, defining special lines:
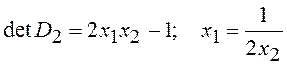 .
.
On fig.1 the graph of function of a
SCC matrix determinant, on fig.2 – the graph of a solution of the equation ![]() are represented.
are represented.
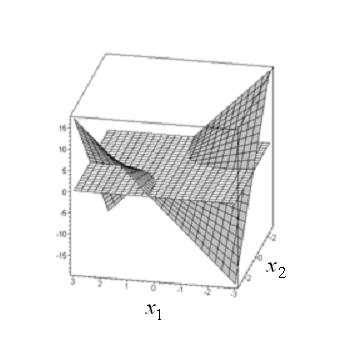
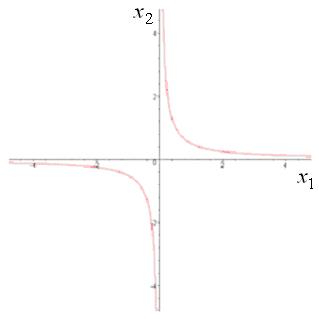
Figure 1. Graphs of ![]() Figure 2. Graph of the solution
Figure 2. Graph of the solution
and zero plane
![]() concerning
concerning ![]()
3. CONCLUSION
In this paper analytical expressions for state commonness condition matrices are derived using differential geometry method. State commonness criterion for affine nonlinear systems of arbitrary order is stated on the base of vector fields commutators (Lie brackets). Particular criterions for the systems of second and third order are defined. Cases when vectors forming state commonness condition matrices do not include control variable are revealed. These cases essentially simplify the qualitative investigation of nonlinear systems behavior.
4. REFERENCES
[1] Methods of Classical and Modern Automation Control Theory: Textbook in 3 volumes. Vol. 3: Methods of Modern Automation Control Theory. / Under the editorship of N.D. Egupov. Moscow.: Publishing house of Bauman MGTU, 2000 (in Russian).
[2] V.A. Oleinikov. Optimal Process Control in Oil and Gas Industries. Leningrad: Nedra, 1982 (in Russian).
[3] F. Warner. Fundamentals of the Smooth Manifolds Theory and Lie Groups. Moscow.: Mir, 1987 (in Russian).
[4] Yu.N. Andreev. Differential Geometry Methods in Control Theory. // Automation and Telemechanics, 1982. № 10. PP. 5-46 (in Russian).
[5] R. Hermann, A.J. Krener. Nonlinear Controllability and Observability. // IEEE Transactions on Automatic Control, Vol. AC-22. No. 5, October 1977. PP. 728-740.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.