Вероятностно-статистический подход к определению расчетных климатических нагрузок на воздушные линии электропередачи, страница 3

 .                                        (5)

Это выражение дает возможность по заданному уровню риска R_τ и времени эксплуатации t найти значение опасного воздействия. Для этого соотношение (5) надо рассматривать как уравнение для определения х_оп.

Для практического применения формулы (5) необходимо получить аналитическое выражение F_X^(у)(x/x³x₀). Это можно сделать многими способами, например, методом наибольшего правдоподобия или, когда метод правдоподобия чрезвычайно громоздок, методом моментов. Поскольку этот метод определения расчётных климатических нагрузок не опирается на теорию порядковых статистик, его можно применить с распределениями, отличными от перечисленных предельных законов распределения. Вместе с тем в качестве F_X^(у)(x/x³x₀) можно также использовать распределения Гумбеля, Фишера-Типпета и Вейбулла.

На рис. 1 приведены алгоритмы расчётов при использовании метода порядковых статистики, лежащего в основе норм проектирования МЭК,  и метода управления рисками в сравнении с методикой расчётов по ПУЭ-7.

Рассмотренные выше методики были опробованы на ряде примеров определения расчётной климатической нагрузки на предполагаемые ВЛ, проходящие вблизи метеостанций Ставропольского края. Также рассмотрен пример индивидуального подхода к проектированию и определены расчётные уровни воздействия на реальную ВЛ межсистемного назначения в ОЭС Волги на основании данных с метеостанций в районе сооружения линии. В каждом случае расчётные значения, полученные рассматриваемыми методами,  сопоставлялись со значениями по ПУЭ-7, полученными на основании карт климатического районирования.

Ниже приведены результаты определения климатических параметров (ветрового давления и толщины стенки гололёда) для расчёта конструктивной части участка ВЛ, проходящей в Саратовской области. Для обработки имелся ряд наблюдений за скоростью ветра, полученных за 21 год  и содержащий 7670 значений. Пересчёт скорости ветра V в ветровое давление Q для последующей статистической обработки проводился по общепринятой формуле:

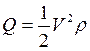, при этом плотность воздуха принималась равной ρ=1.23 кг/м³.

На рис. 2 приведено регистрационное поле наблюдений для ветрового давления. Красным маркером обозначены точки, соответствующие максимальным скоростям ветра в пределах каждого года наблюдений. Абсолютный максимум скорости ветра 23 м/с был зарегистрирован в 1992 году.

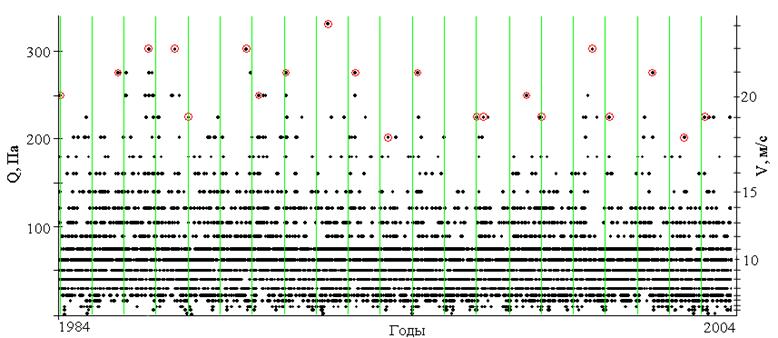
Рисунок 2. Регистрационное поле скорости ветра.

Гистограмма ветрового давления, приведённая на рис. 3, наглядно иллюстрирует тот факт, что бόльшая часть зарегистрированных скоростей ветра лежит в области, соответствующей малому ветровому давлению: в 82% случаев Q < 90 Па (V < 12 м/с). Область, соответствующая значительным скоростям ветра (7 и более баллов по шкале Бофорта), на которые должны быть рассчитаны конструкции ВЛ, представляет собой редкие значения в вытянутой части гистограммы.  Из значений ветрового давления в этой области формируется выборка во втором из описанных выше методов определения расчётных нагрузок.

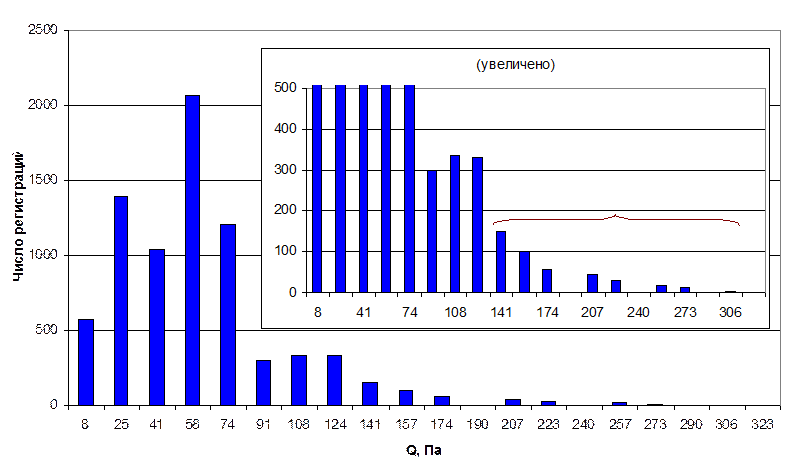Рисунок 3. Гистограмма ветрового давления

Пороговое значение ветрового давления при применении второго метода варьировалось в диапазоне 140…180 Па (скорость ветра – 15…17 м/с), а размер выборки при этом менялся от 415 до 165 значения (5.4…3.5% от общего числа значений). Для аналитического описания вероятностного поведения ветровой нагрузки рассматривались несколько ФРВ: Гумбеля, Вейбулла, γ- и β-распределение. Построение серии зависимостей по выражению (5) для этих четырёх законов распределения определяло интервал расчётных значений с небольшим разбросом.