Во-вторых, после определения ФРВ для максимальных нагрузок Fп(x) вводится в рассмотрение [5] условный период повторяемости максимальных нагрузок в соответствии со следующим выражением:
.
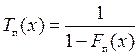(2)
Как видно из приведенного выражения, период повторяемости обратно пропорционален вероятности превышения принятого уровня максимальных нагрузок х.
Соответственно вероятность Р1(х) превышения уровня воздействия, равного х, в течение одного года будет равна
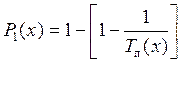, а в течение срока эксплуатации
объекта длительностью τ лет –
.
(3)
Международная электротехническая комиссия (МЭК) рассматривает три уровня надежности при проектировании ВЛ [6]. Первый уровень предусматривает период повторяемости нагрузки 50 лет, что соответствует вероятности превышения расчетной нагрузки за один год P1 = 0.02, а за 50 лет – 0.632; второй уровень соответствует периоду повторяемости 150 лет, т.е. вероятности превышения расчетной нагрузки за год P2 = 0.0067, а за 50 лет – 0.295; третий – периоду повторяемости 500 лет и вероятности превышения расчетной нагрузки за годP3 = 0.002, а за 50 лет эксплуатации – 0.095.
При заданном уровне надежности расчетная нагрузка определяется из (3) следующим образом:
где Fп-1 – функция, обратная к ФРВ и определяемая для всех перечисленных выше ФРВ путем несложных преобразований.
Определённым недостатком изложенного подхода является то обстоятельство, что он оперирует только годовыми максимумами воздействий. При этом годы с одинаковыми максимумами, но различной интенсивностью воздействия, рассматриваются как одинаковые. Это, по-видимому, в статистическом отношении приводит к неточностям в оценке реальных условий работы ВЛ и следует считать упрощающим допущением. Другим недостатком является отсутствие в теории вероятностей аналога понятию периода повторяемости, определяемого по формуле (2).
При подходе, основанном на теории управления риском [2], исходный ряд данных (1) также замещается сокращенной выборкой. Но вместо годовых максимумов выделяется некоторая доминирующая составляющая случайного процесса: рассматриваются случайные события {X(t)≥x0}, где x0 – некоторое пороговое значение неблагоприятной нагрузки. В результате в рассмотрение вводятся только те значения
,
(4)
которые удовлетворяют неравенству хi ³ х0. Тем самым вместо всего диапазона случайной выборки (1) рассматривается так называемый хвост распределения этой выборки [2].
Выбор x0 осуществляется так, чтобы в полученной выборке значимых воздействий (4) содержалось 5-10% от общего числа наблюдений. Тем самым производится отказ от применения в качестве исходной информации исключительно годовых максимумов, учитываются все случаи наличия экстремальных нагрузок без отнесения их к определенному интервалу времени, a малые годичные экстремумы совсем не рассматриваются.
Если x0 достаточно велико, поток событий {X(t)≥x0} можно рассматривать как случайный поток событий, для описания которого можно использовать распределение Пуассона. При этом вероятность того, что на этом отрезке произойдет ровно m событий указанного вида, равна
, где 
, а λ(t) – мгновенная плотность потока
рассматриваемых событий.
При постоянном l(t) = l0 получаем 
. В общем случае на основе теоремы о
среднем получаем 
, где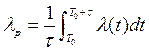 
. При
этом интенсивность lр оценивается
по формуле: 
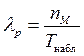, где nM – число наблюдений в (1), для
которых справедливо неравенство x³x0.
Пусть Fx(у)(x) есть условная функция распределения воздействия Х
при условии, что Х ³ х0: 
.
Обозначим через хоп искомое опасное значение климатической нагрузки. По аналогии с [7] риск превышения этого уровня в течение времени τ эксплуатации энергообъекта определяется по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.