Моделирование систем массового обслуживания

9. Системы массового обслуживания

9.9. Моделирование систем массового обслуживания

Задачи, встречающиеся на практике, зачастую оказываются настолько сложными, что получить их характеристики с помощью аналитического метода невозможно (например, поток поступающих требований не является простейшим, время обслуживания не распределено по показательному закону, дисциплина обслуживания может быть достаточно сложной, кроме того, в системе могут существовать обратные связи и т.д.). В таких случаях целесообразно использовать метод моделирования СМО, справляющийся с перечисленными трудностями. Если процесс функционирования СМО случайный, то моделирование подобной системы состоит в построении реализаций случайного процесса.

Метод статистических испытаний позволяет исследовать зависимость эффективности системы обслуживания от параметров потока заявок и самой системы. Кроме того, этот метод позволяет оценить не только простейшие характеристики эффективности системы, но значения многих других важных показателей системы (дисперсию доли отказов, вероятность того, что значение доли отказов будет не ниже заданного и т.п.).

Сущность метода статистических испытаний применительно к анализу СМО состоит в следующем. С помощью специальных алгоритмов формируются реализации потока заявок с заданным законом распределения интервалов между заявками. Далее моделируется процесс функционирования обслуживающей системы. Все интересующие показатели работы системы фиксируются. Общий алгоритм модели многократно воспроизводит случайные реализации процесса функционирования системы при некоторых заранее заданных условиях. Накопленная в результате информация статистически обрабатывается.

Входящий поток требований однозначно задается последовательностью моментов времени поступления заявок в систему T₁, T₂, ... Однако для моделирования удобнее рассматривать случайные величины , определяющие длину интервалов между моментами поступления заявок. Тогда для задания входящего потока достаточно получить последовательность случайных величин  с заданным законом распределения.

Пусть, например, на вход системы поступает простейший поток. Плотность распределения длин интервалов между заявками для такого потока соответствует показательному закону:

Тогда, как отмечалось, для получения последовательности чисел  используется соотношение

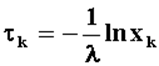
где х_i- i-е случайное число из последовательности с равномерным распределением из интервала (0, 1).

Аналогично может быть получена последовательность и для каких либо других законов распределения длин интервалов между заявками.

Те же приемы используются и для формирования случайных значений времени обслуживания.

Рассмотрим одну из простых систем массового обслуживания, которая состоит из 3 одинаковых каналов; входящий поток - простейший с параметром l; время обслуживания в канале одного требования постоянно и равно . Система без ожидания, т.е. требование, заставшее все каналы занятыми, покидает систему. Дисциплина обслуживания такова: если в момент поступления k-гo требования, первый канал свободен, то он приступает к обслуживанию требования; если этот канал занят, то требование обслуживает второй канал и т.д. Требуется определить, сколько требований в среднем обслужит система за время Т и сколько в среднем она даст отказов?

За начальный момент расчета выбирают момент поступления первого требования . Введем следующие обозначения:

- момент поступления k-го  требования;

- промежуток времени между поступлением в систему