Методы оптимизации: Методическое пособие для самостоятельного изучения курса и подготовки к экзаменам

А.Б.Бушуев

®

Методы оптимизации

Методическое  пособие           

Санкт-Петербург

2003

Методическое пособие предназначено для студентов специальности "Системы управления и информатика" вечернего факультета по дисциплине "Методы оптимизации".

В пособии рассматриваются методы решения многомерных задач линейного и нелинейного программирования, специфические задачи одномерного поиска экстремума, а также теория матричных игр, использующая математический аппарат задач линейного программирования. Приведены примеры и программы решения экстремальных задач в программной среде "Маткад".

Пособие базируется на знаниях, полученных студентами в курсах математики и вычислительной техники.

Может быть рекомендовано для самостоятельного изучения курса "Методы оптимизации" и для подготовки к экзаменам.                                        

Содержание

Введение .............................................................................

1. Одномерный поиск экстремума

1.1.  Унимодальная функция и интервал неопределенности

1.2.  Минимаксная стратегия

1.3.  Пассивный поиск

1.4. Последовательный поиск

1.4.1. Метод половинного деления

1.4.2. Метод чисел Фибоначчи

1.4.3. Метод "золотого сечения"

2.    Многомерный поиск экстремума.

2.1.Постановка задач линейного и нелинейного программирования

2.2. Безусловный экстремум

2.3. Задачи линейного программирования

2.3.1.Задача об распределении ресурсов

2.3.2. Задача о перевозке грузов

2.3.3. Геометрическое пояснение задач линейного программирования

2.3.4.Симплекс-метод

2.4. Задачи нелинейного программирования

2.4.1.Метод неопределенных множителей Лагранжа.

2.4.2. Задача Куна-Таккера

3.   Теория  матричных игр

3.1. Игры с нулевой суммой

3.2. Смешанные стратегии

3.3. Рандомизированное управление

3.4. Двухсторонняя монополия как задача теории игр

Литература

Введение

Методы оптимизации широко используются в теории управления для нахождения наилучшего в некотором смысле протекания процесса, наилучшей организации системы управления, наилучшмх ее параметров.

Математически задача оптимизации ставится следующим образом. Задается целевая функция (или критерий), например, f=f(x) или J=J(x), т.е. функция, зависящая от аргумента х. Необходимо найти такое значение х=х* , которое дает экстремальное значение (минимум или максимум) функции f=f(x) или J=J(x). Именно значение аргумента х=х*  является ответом задачи оптимизации,  поскольку затем найти значение экстремума  f(х*) или J(х*) не представляет труда.

Например, пусть необходимо управлять некоторым объектом - самолетом. Сначала ставим задачу управления - самолет должен перелететь с одного аэродрома на  другой как можно быстрее. Для решения этой задачи сначала надо выбрать траекторию полета, т.е. задать во времени изменение высоты полета Н, скорость V, угол курса Θ.

Для решения задачи оптимизации составим целевую функцию, в качестве которой выберем время полета Т, т.е. зададим Т=Т(Н,V,Θ).

Теперь найдем такие  Н, V и Θ, которые дают минимальное значение времени полета Т. Тем самым мы найдем оптимальную траекторию  полета. Такая задача называется задачей максимального быстродействия и она может быть решена перед началом полета.

Оптимальной траектории полета соответствуют определенные значения углов поворота рулей самолета. Если пилот установит эти значения углов поворота рулей, то это не значит, что самолет полетит по оптимальной траектории максимального быстродействия. Дело в том, что на самолет во время полета действуют внешние помехи, вредные возмущения, прежде всего, слечайные порывы ветра, которые сносят его с оптимальной траектории. Поэтому во время полета нужно решать задачу нахождения таких значений углов поворота рулей самолета, при котором вектор Δ отклонений самолета от оптимальной траектории 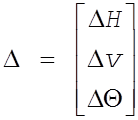 за все время полета был бы минимальным. Такая задача называется задачей минимизации ошибок.

Если самолет летит в автоматическом режиме, под управлением автопилота, то задача оптимизации  позволяет найти конструктивные параметры автопилота, обеспечивающие минимум ошибок.

Есть множество и других задач в теории управления, в которых используются методы оптимизации.

1. Одномерный поиск экстремума

1.1. Унимодальная функция и интервал неопределенности

Одномерный поиск означает решение задачи оптимизации, в которой целевая функция зависит от скалярного аргумента. Если аргумент является векторным, то поиск экстремума называется многомерным.

Обычно методы поиска рассматриваются для решения задачи минимума целевой функции f(x). Если надо найти максимум функции f(x), то обычно ей приписывают знак "минус" и используют методы поиска минимума. Значение аргумента х* будет определять точку минимума для -f(x) и точку максимума для f(x).

Далее будем рассматривать задачи нахождения минимума унимодальных функций.

Определение. Функция f(x) называется унимодальной на промежутке [a,b], xÎ [a,b], если на этом промежутке она имеет одно минимальное значение ( а точнее, точную нижнюю грань).

Унимодальная функция может иметь разрывы первого рода. Примеры  функций, унимодальных на  [a,b],  приведены на рис.1. Минимум первой кривой находится в точке х1*, минимум второй кривой - в точке х2*, минимум третьей и четвертой кривых находится на границе участка в точке х3*=b.

Примеры функций, неунимодальных на [a,b],  приведены на рис.2.

Функция 5 имеет два минимальных значения, а функция 6 имеет бесконечное множество минимальных значений.

В реальных задачах управления часто зависимость f(x) неизвестна. Известно только, что f(x) имеет минимум при xÎ [a,b]. Поэтому точка минимума ищется путем проведения экспериментов на реальной системе управления.

    

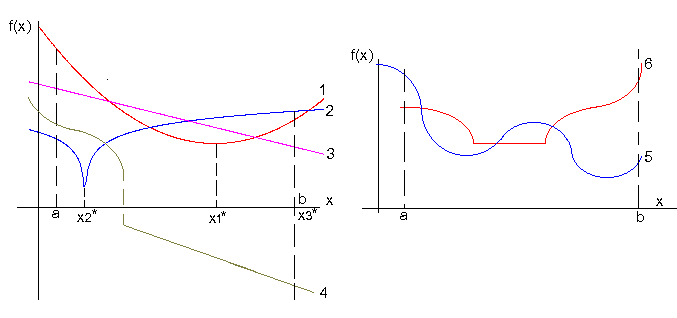
Рис.1                                               Рис.2

Например, пусть мощность Рп электрических потерь некоторого электрического двигателя зависит от частоты ω переменного