Синтез наблюдающего устройства Люенбергера. Синтез наблюдателя (фильтра) Калмана

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Кафедра систем управления и информатики

Расчетно-исследовательская работа

«Синтез наблюдателей Люенбергера и Калмана

Выполнил: Васильев В. И.

Группа: 5147

Преподаватель: Коровьяков А. Н.

Санкт-Петербург

2007

Дана модель гипотетического самолета с параметрами:

Этап I				Этап II
		, [c]	, %
2.4	3.4	1.2	19	1.2	2.4	0.6

1.  Синтез наблюдающего устройства Люенбергера.

Структурная схема модели гипотетического самолета:

,      ,         

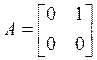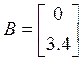Полином Баттерворта 2-го порядка с tп=2.9с

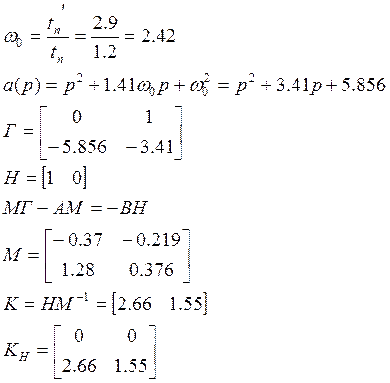
Проверка системы на наблюдаемость:

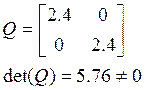
Система полностью наблюдаема.

Синтез устройства оценки полной размерности:

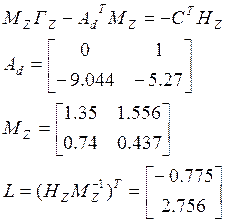
Уравнение движения устройства оценки полной размерности:

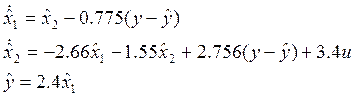
Оценка параметра экспоненциальной устойчивости процесса наблюдения по норме вектора ошибки оценивания.

Система относительно вектора ошибки оценивания (вектора невязки) имеет вид:

Модель ошибок наблюдения:

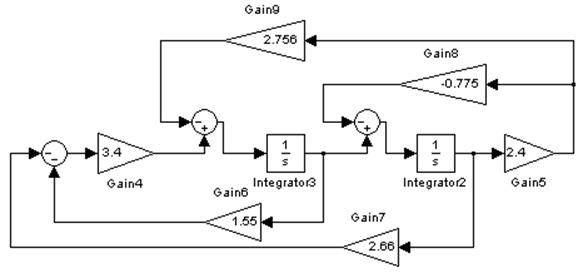
График :

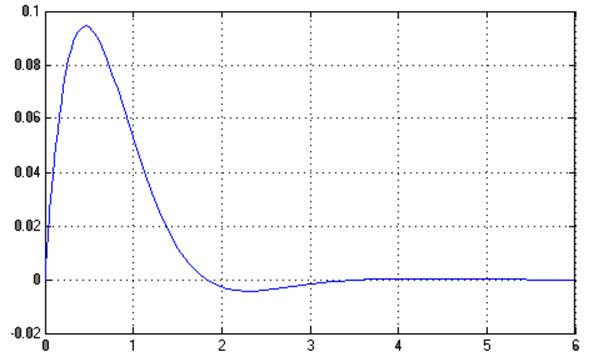
График :

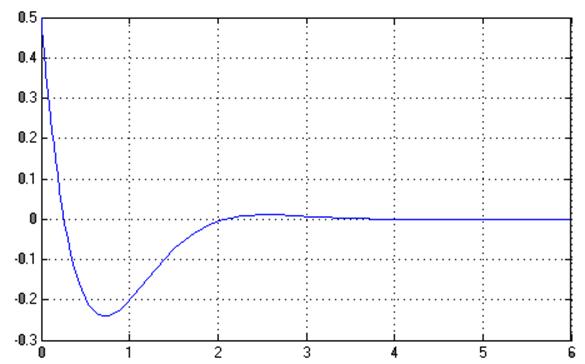
Решение ищется как

Характеристический полином матрицы  :

Найдем степень устойчивости системы:

Если собственные числа матрицы  удовлетворяют условию , то найдется матрица  такая, что для любых t>0 . Данное свойство устанавливает экспоненциальную устойчивость системы  с параметром α, который определяет скорость затухания процессов. Параметр зависит от расположения собственных чисел  на комплексной плоскости и выбирается меньшим, чем степень устойчивости, т.е. .

Таким образом, получаем параметр экспоненциальной устойчивости процесса наблюдения по норме вектора ошибки оценивания:

Свойства синтезированного наблюдателя.

Задача наблюдения – это задача синтеза алгоритма, обеспечивающего оценивание переменных состояния объекта, которые невозможно непосредственно измерить. В данной работе такими переменными являются координата положения и скорость самолета.

Наблюдатель Люенбергера обеспечивает восстановление этих переменных состояния из измеренных входных и выходных переменных. Оценка вектора состояния – это вектор-функция, которая с течением времени стремится к оцениваемому значению вектора состояния. Вектор невязки при этом должен стремиться к нулю.

2. Синтез наблюдателя (фильтра) Калмана.

Структурная схема модели гипотетического самолета:

,      ,         ,          

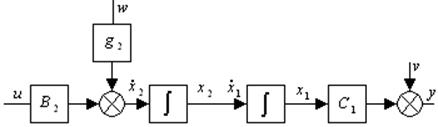
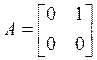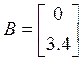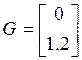
Полином Баттерворта 2-го порядка с tп=2.9с

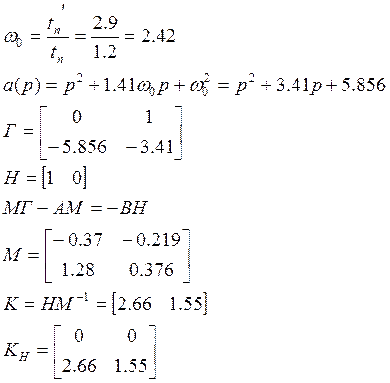
Проверка системы на наблюдаемость:

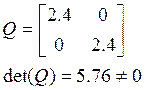
Система полностью наблюдаема.

Синтез устройства оценки полной размерности:

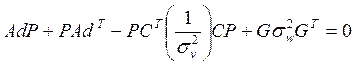
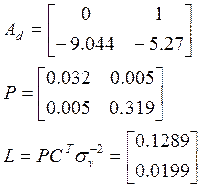
Уравнение движения устройства оценки полной размерности:

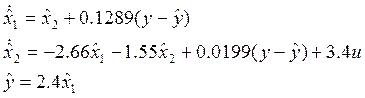
Оценка параметра экспоненциальной устойчивости процесса наблюдения по норме вектора ошибки оценивания.

Система относительно вектора ошибки оценивания (вектора невязки) имеет вид:

Модель ошибок наблюдения:

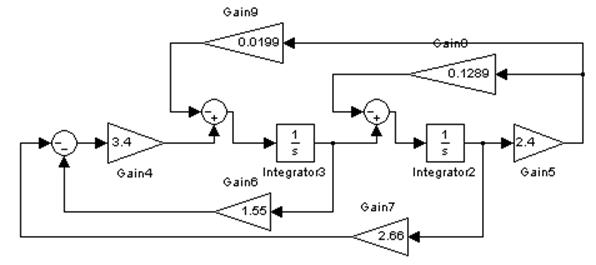
График :

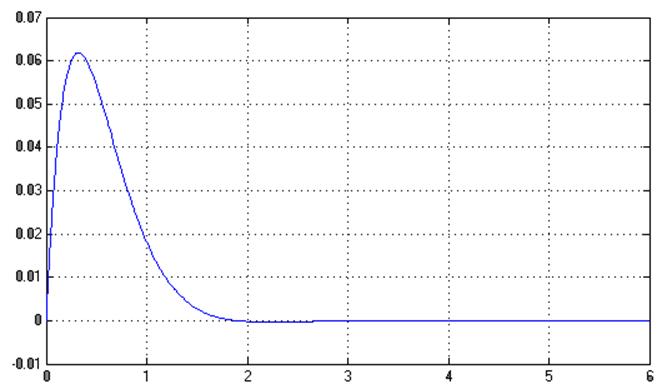
График :

Решение ищется как

Характеристический полином матрицы  :

Найдем степень устойчивости системы:

Если собственные числа матрицы  удовлетворяют условию , то найдется матрица  такая, что для любых t>0 . Данное свойство устанавливает экспоненциальную устойчивость системы  с параметром α, который определяет скорость затухания процессов. Параметр зависит от расположения собственных чисел  на комплексной плоскости и выбирается меньшим, чем степень устойчивости, т.е. .

Таким образом, получаем параметр экспоненциальной устойчивости процесса наблюдения по норме вектора ошибки оценивания: .

Свойства синтезированного наблюдателя.

Наблюдатель Калмана обладает такими же свойствами, как наблюдатель Люенбергера, за исключением того, что он работает в условиях действия случайных возмущений на входе и выходе объекта (фильтрует возмущения).

3.  Моделирование на ЭВМ наблюдателей Люенбергера и Калмана.

Моделирование наблюдателя Люенбергера.

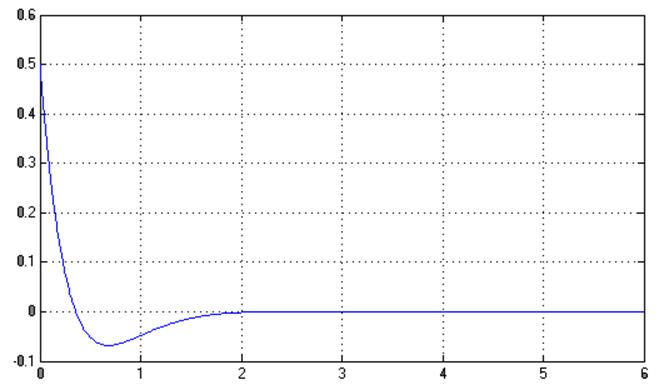
Структурная схема ОУ и наблюдателя Люенбергера для него:

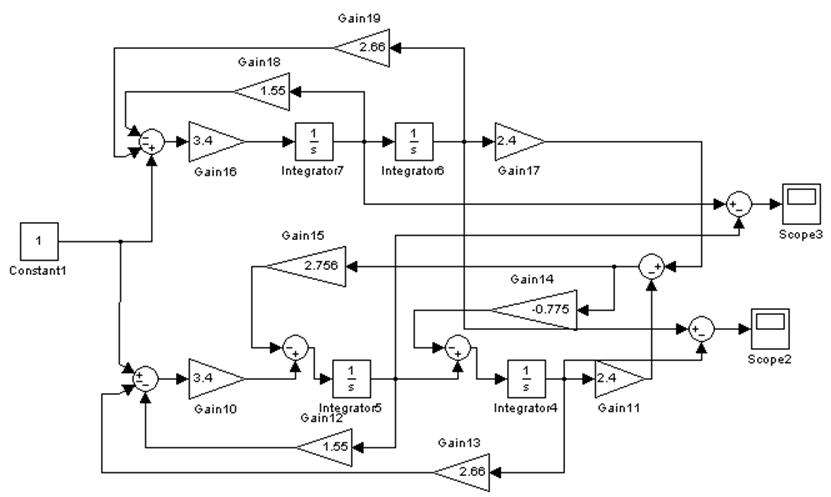
График :

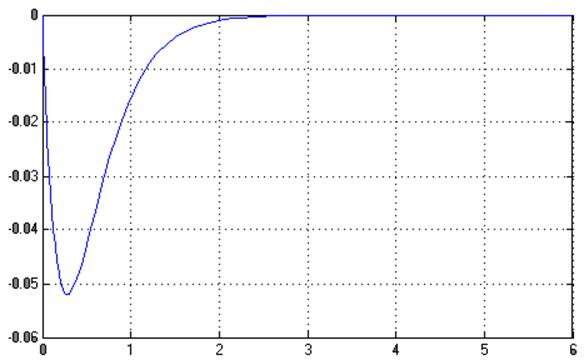
График :

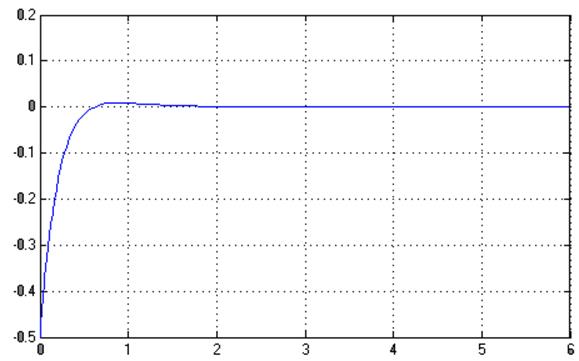
Графики , :

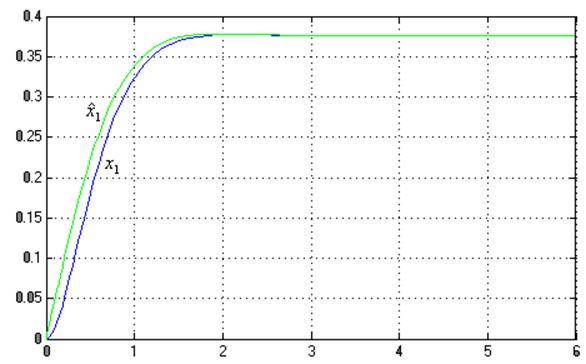
Графики , :

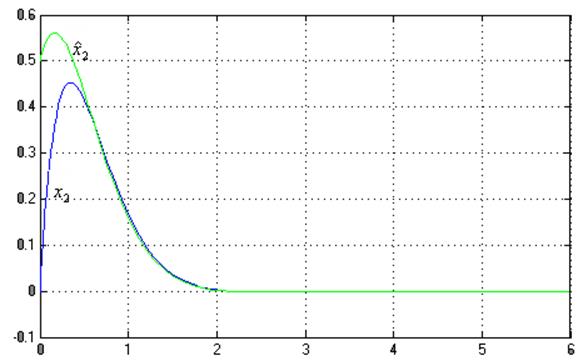
Моделирование наблюдателя Калмана.

Структурная схема ОУ и наблюдателя Калмана для него:

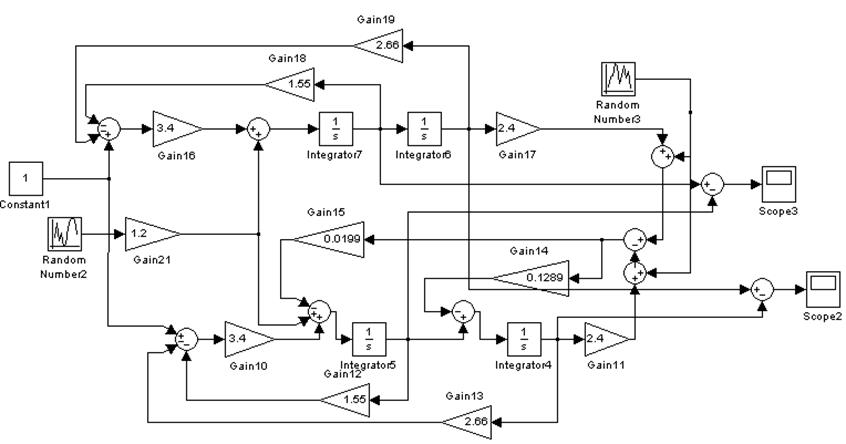
График :

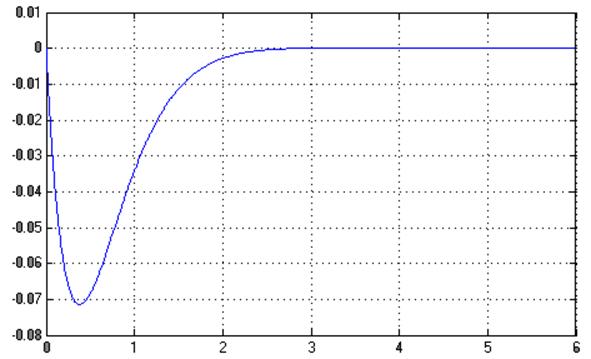
График :

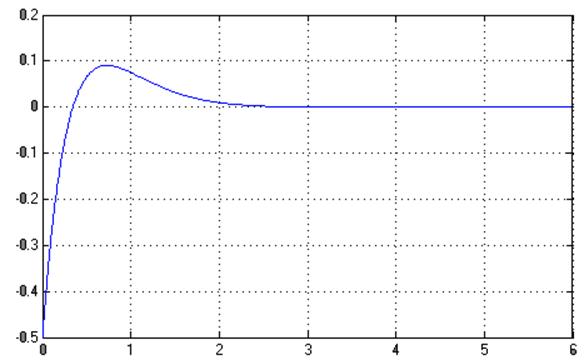
Графики , :

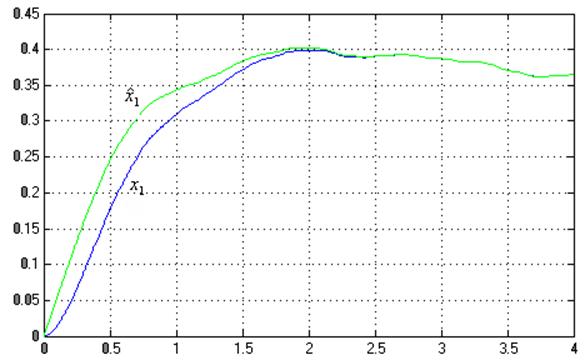
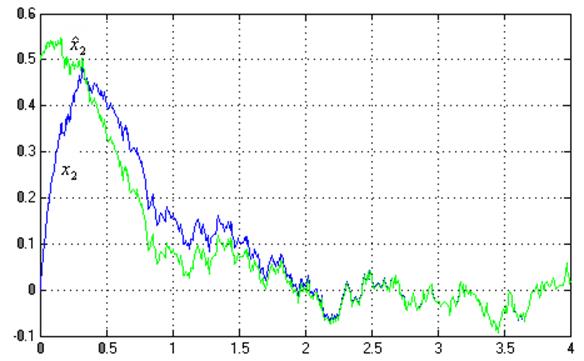
Графики , :

Структурные схемы обоих наблюдателей идентичны и отличаются только коэффициентами L.

Как видно из графиков, динамические и статистические свойства систем с различными наблюдателями совпадают с незначительными отклонениями.

Для моделирования случайных возмущений использовались генераторы шумов, которые вводили случайные изменения параметров модели.

Выводы: В данной расчетно-исследовательской работе был произведен синтез устройств оценки полной размерности переменных состояния полета