Ответы на экзаменационные вопросы № 1-33 дисциплины "Теория вероятностей и математическая статистика" (Определенность и неопределенность научного познания. Понятие доверительной вероятности и доверительного интервала)

предшествующего t₀ – периода, иначе говоря они не зависят от того отказывала ли система в прошлом.

2) Если время отказа является равномерным потоком, то они подчинены показательному закону распределения.

ПРИМЕР:

Попадание метеорита в космическую станцию не как не зависит от того попадали ли метеориты в ближайшее время, иначе говоря ретроспективы не играют роль.

22. Центральная предельная теорема А. М. Лепунова

В реальной действительности на некоторые явления, события или процесс оказывает влияние большое число факторов, часть из которых, возможно, является мало значительной. Можно утверждать что если число воздействующих СВ достаточно велико и не одна из них не оказывает подавляющее значения, то случайное явление подчинено нормальному закону распределения СВ.

Этот факт определяется центральной предельной теоремой Лепунова.

Теорема: Если имеется достаточно большое СВ х₁, х₂, х₃,…,х_i, x_n, где i – текущий индекс, то значение суммы этих СВ при условии что ни одна из них не оказывает подавляющего влияния распределения как угодно близко к нормальному закону распределения СВ, причем тем больше, чем больше число n.

Следует отметить, что СВ представляет собой сумму. СВ могут быть распределены по любым законам распределения в отдельности, однако их сумма при оговоренных условиях даст нормальные значения.

Нормальный закон распределения образует колокообразную форму, которая в наилучшей степени отражается холмиком песчинок в песочных часах. Другим аналогом является потребление электроэнергии в большом доме, не зависимо от поведения потребителя. Однако, если в этом же доме разместить вычислительный центр, то нарушаться условия центральной предельной теоремы (один из потребителей во много раз превосходит других).

Сам термин нормальный закон распределения не совсем удачен, однако он подчеркивает что суммирование любых законов распределения приводит в итоге к нормальному закону распределения, который является всеобщим законом распределения.

22. Закон нормального распределения СВ (закон Гаусса)

Нормальный закон распределения ранее был хорошо описан Гауссом и поэтому часто называется гауссово распределение.

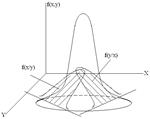
Нормальный закон распределения описывается относительно сложным выражением, подчеркивающим его колокообразную форму с ассимтатическими затухающими хвостами.

Таким образом, видим что нормальный закон распределения зависит от двух параметров: m_x, σ_x.

В ряде случаев нормальный закон центрируется, т.е. переносится в точку отсчета координат.

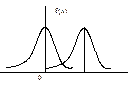
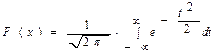 - для центрированного значения

Для нормального закона распределения: , где

В этом выражении подынтегральная функция называется интегралом Лапласа и он относится к неберущемся, поэтому он табуирован и представлен в таблицах. Тогда вероятность попадания СВ в интервал [a,b]:

, где Ф – значение интеграла Лапласа.

Это обусловлено тем, что:

1)  µ1=0

2)  µ2=σx(в квадрате)=Dx

3)  µ3=0 A3=0

4)  µ4=3σ(в четвертой степени)  

23. Свойства плотности распределения

1) Плотность распределения нормального закона распределена всём интервале [-∞;+∞] и является положительной величиной, т.к. первая производная от функции распределения F(х) является положительной (возрастает).

2) Плотность распределения симметрична относительно МО, т.к. отклонение (x-m_x)² симметрично.

3) Плотность распределения имеет максимальное значение, равное:

4) Плотность распределения асимптотически приближается к оси абсцисс при х→±∞

5) Плотность распределения имеет 2 точки перегиба

6) При изменении МО, но не измены СКО, нормальный ЗР смещается вдоль оси абсцисс.

m_x = var; σ_x=const

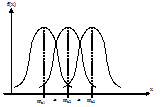
7) Если изменяется СКО, но МО – неизменно, то:

m_x = const; σ_x=var

Форма кривой уплощается, т.к. площадь, ограниченная плотностью распределения есть вероятность, всегда равная 1.

В целом эти свойства в значительной степени повторяют общие свойства плотности распределения.

23. Правило трех σ

Нормальный ЗР обладает замечательным свойством, которое состоит в том, что можно определить вероятность попадания СВ в некоторый интервал, измеряемый количеством укладывающихся в него СКО.

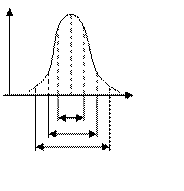
p(m_x-σ_x < X < m_x+σ_x) = 0.682

p(m_x-2σ_x < X < m_x+2σ_x) = 0.954

p(m_x-3σ_x < X < m_x+3σ_x) = 0.997

Отсюда следует, что, если опираться на интервал [m_x±3σ_x], то с практической достоверностью (997 шансов 1000) СВ будет находиться в этом интервале. Это надежная вероятность.

В электроэнергетике часто принимается меньшее значение [m_x±2,5σ_x], что дает вероятность 0,99 (990/1000). В большинстве инженерных дисциплин принимается интервал [m_x±2σ_x], что дает вероятность 0,95. Эта величина считается инженерной вероятностью.

24. Функция одной СВ и её распределение

В ряде случаев для СВ возникает задача определения ЗР СВ «Y», являющейся функцией от «Х»:

Y = φ(X)

Эта задача решается по-разному: является ли СВ «Х» ДСВ, или НСВ:

1) В первом случае, для ДСВ, СВ «Х» задается рядом распределения. Без утраты для общности рассмотрим решение, когда Y = φ(X²), тогда:

Пусть х₁=2, х₂=3

р₁=0.8; p₂=0.2

р(Х=х₁)=0,8, тогда Y1=4, Y2=9, при этом вероятности для Y сохраняется.

2) Для НСВ необходимо, чтобы функция была дифференцируема, при этом необходимо использовать следующую форму:

g(Y) = f(γ(y)·|γ(y)|’_y) (*)

Алгоритм решения таков:

1) Записывается Y = φ(X)

2) Находится функция, обратная Х, как некоторая γ, тогда Y = φ(γ)

3) Определяется плотность распределения от обратной функции: φ(γ)

4) Определяется абсолютная величина производной от обратной функции

5) Полученные значения подставляются в исходную формулу (*)

24. Композиция ЗР

Если некоторая СВ и ее ЗР зависит от ЗР других СВ, имеющих какие угодно ЗР, то эти ЗР складываются. Если, при этом ЗР комбинированной СВ не изменяется, то композиция называется устойчивой. В противном случае, если ЗР комбинированной СВ не соответствует исходной, то композиция считается неустойчивой.

, где z=X+Y

Например, сложение 2-х равномерных ЗР дает закон Симпсона – треугольный ЗР.

В самом общем случае композиция любого числа законов с любым распределением даёт нормальный ЗР.

25. Понятие системы двух СВ

В реальной действительности возникают условия, когда результатом опыта является не одна, а две СВ, иногда и более. В этом случае каждая из СВ «X, Y» принимает то, или иное значение.

СВ (X, Y) = p(X=x₁, Y=y₁)

В этом случае СВ называется двумерной, или системой двух СВ.

ПРИМЕР:

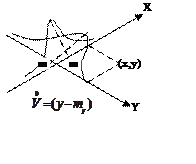
Здесь Х – отклонение по дальности; Y – боковое отклонение

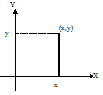На плоскости:

25. ЗР системы двух СВ

В отличие от одномерной СВ (каждому значению СВ соответствует значение вероятности) ЗР двумерной СВ представляет собой таблицу:

где i = 1,2,3, … ,n

j = 1,2,3, … ,m

В каждой строке идет суммирование произведений некоторого постоянного значения Х, например х₁, при вариации случайных значений СВ Y (у₁, у₂, … , y_j, … , y_m). Подобная картина соответствует столбцам, где при неизменном значении Y, например у₁, при вариации значения СВ X (х₁, х₂, … , х_i, … , x_m). Совпадения значений на пересечении строк и столбцов {p(x_i∙y_j)} соответствует некоторому значению двумерной СВ. Правило проверки для системы двух СВ являются условия, что сумма всех вероятностей равна 1, если события не совместны

ЗР двумерной СВ является ее наиболее полноценной характеристикой, однако, как и в случае с одномерными СВ приходится вводить некоторые новые характеристики.

26. Функция распределения системы двух СВ

Подобно одномерному случаю, функция распределения двумерной СВ есть вероятность того, что СВ «Х» примет значение меньше некоторого «х», а «Y» будет меньше «у».

F(x) = p(X<x)

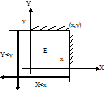F(x,y) = p(X<x, Y<y)

Это означает, что любая взятая произвольно точка будет лежать левее и ниже точки х,у, вплоть до (-∞), иначе говоря, эта точка будет принадлежать некоторому квадранту Е.

Функция распределения двумерной СВ очёркивается т.о. в декартовой системе координат некоторыми ортогонально расположенными векторами. (по «х», и по «у»).

26. Свойства двумерной СВ

Эти свойства в значительной степени подобны свойствам одномерной функции распределения: 1) Функция распределения F(x,y) является положительной функцией

0≤F(x,y)≤1 Доказательство:

Вытекает из свойства вероятности 2) Функция распределения F(x,y) является неубывающей функцией своих аргументов F(x2,y)>F(x1,y);

F(y2,x)>F(y1,x); ДОКАЗАТЕЛЬСТВО:Вытекает из того, чем правее будет выбрана х, тем больше вероятность попадания СВ слева (см. рисунок).Одновременно, чем больше у, тем выше верхняя граница квадранта Е, тем больше вероятность попадания в этот квадрант.3) Исходя из возможных значений (х,у) можно получить ряд предельных соответствий.

3.1)

3.2)

3.3)

Доказательство:

При смещении границ квадранта Е в (-∞), квадрант скукоживается до точки, что приводит к невозможности определения вероятности.

3.4)

Доказательство:

При сдвиге границ вправо и вверх любая случайная точка с вероятностью 1 окажется левее и ниже, т.к. квадрант Е занимает всю возможную площадь.

27. Плотность распределения вероятностей двумерной СВ

Выше была рассмотрена функция распределения двумерной СВ F(x,y). Основные свойства этой функции распределения в значительной степени аналогичны одномерной функции СВ F(x).

Однако, как и в одномерном случае определение вероятности более удобно выполнять по плотности распределения.

Плотностью распределения вероятности двумерной СВ называется предел отношения вероятности попадания СВ в элементарный прямоугольник ΔR к площади этого прямоугольника, когда последний стягивается в точку.

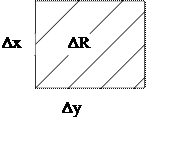
Это соответствует понятию производной, переходя к ней получим плотность распределения двумерной СВ:

Значит, плотность распределения вероятности системы СВ есть вторая смешанная частная производная от двумерной функции распределения по ее аргументу.

27. Свойства плотности распределения

Эти свойства в основном повторяют свойства одномерной плотности распределения.

1) f(x,y) ≥ 0

2) Объём, ограниченный плотностью распределения определяет достоверное событие, вероятность которого равна 0.

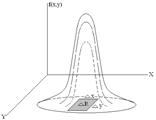
3) Для получения одномерной плотности распределения по х, или по у, необходимо аргумент второй функции устремить в ∞ (см. свойства функции распределения).

Тогда частная плотность распределения одной из СВ X, или Y есть несобственный интеграл в бесконечных пределах от двумерной плотности распределения по другому аргументу:

Следовательно, для получения частной плотности распределения при известной двумерной необходимо взять интеграл от двумерной по другому аргументу.

28.  Условная плотность распределения

По аналогии с одномерными величинами и условной вероятностью для двумерных СВ вводится условная плотность распределения. Она показывает как наступление одного из случайных событий влияет на вероятность наступления другого события. Раньше было так: p(AB) = p(B) ∙ p(A/B) Это именно то, что нам нужно, только в качестве второго события выступает другая СВ. Тогда условная плотность распределения:

По аналогии с одномерной функцией можно ввести понятие зависимости и независимости СВ, а именно: если условная плотность распределения равна безусловной, то СВ независимые.

Условие независимости СВ:

f(x,y) = f_X(x)∙f_Y(y)

Условная плотность распределения является чрезвычайно важной характеристикой для технических систем.

ПРИМЕР: рост и вес X и Y являются системой СВ.

Существует статистическая зависимость этих величин, тогда условная плотность распределения может показать как у людей одного и того же роста распределяется функция распределения веса.

29. Числовые характеристики двумерных СВ (или системы двух СВ)

По аналогии со случайными величинами для системы двух СВ могут быть определены некоторые числовые характеристики, которые являются некоторым косвенным эквивалентом ЗР, а именно МО для X и Y и дисперсия для X и Y.

Используются те же самые формулы с заменой f(x) на f(x,y) и соответственно f(y) на f(x,y).

Для ДСВ двойное интегрирование заменяется суммой, а dx и dy вероятностью p(x_i,y_j).

Аналогичные характеристики могут быть вычислены для условных плотностей распределения:

30. Корреляция двух СВ

Две СВ, входящие в систему могут быть статически связаны, т.е. оказывать друг на друга взаимное влияние. Такая статистическая связь не является строго причинным следствием и характеризуется ИВ термином «корреляционная связь», или «корреляционная зависимость». Другое определение – ковариация. В физических смыслах, этот термин состоит в том, что одна из СВ случайно флуктуирует, т.е. имеет вариацию, другая тоже, тогда их взаимная согласованная вариация есть ковариация. Это свойство системы двух СВ определяется корреляционным моментом:

Таким образом, корреляционный момент есть МО произведения отклонения СВ X и Y от своих МО. K_xy = K_yx Для НСВ:

Ковариация является важнейшей характеристикой отношения двух СВ, при этом ковариация двух независимых величин равна 0. Это правило означает, что, если СВ независимые, то их ковариация равна 0, однако обратное – неверно.

31.  Важное уточнение свойств числовых характеристик в случае их зависимости

1) M[X∙Y] = M[X] ∙ M[Y] + K_xy

2) D[X+Y] = D[X] + D[Y] + 2K_xy

31. Коэффициент корреляции

Ковариация (cov) не удобна тем, что имеет размерность произведения двух СВ. В связи с этим вводится безразмерная СВ – коэффициент корреляции.

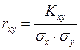    K_xy ≤ σx ∙ σy: -1≤r_xy≤1

Коэффициент корреляции показывает уровень статистической связи, причем линейной статистической связью.

Y = a∙X, тогда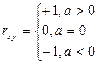

r_xy = (sign)a

(сигнума)

Физический смысл коэффициента корреляции такой:

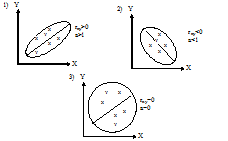
ПРИМЕР1: Тяга ракетного двигателя является случайной, т.к. зависит от качества топлива, технологических отклонений и др. Расстояние, которое пролетит ракета за одно и то же время тоже является СВ, при этом, чем больше тяга, тем больше расстояние пролетит ракета, r_xy > 0.

ПРИМЕР2: В электрических системах величина тока короткого замыкания является СВ, наряду с этим время отключения короткого замыкания с помощью релейной защиты также имеет вариацию, тогда, чем больше ток короткого замыкания, тем быстрее он отключится, r_xy < 0.

ПРИМЕР3: При подготовке к экзамену студент делит время на две части: 1) читает конспекты; 2) смотрит ТВ. Чем больше он читает конспект, тем меньше он смотрит ТВ, r_xy < 0. Наряду с этим, чем больше он читает конспект, тем лучше он сдаст экзамен r_xy > 0. Это свидетельствует о том, что одна и та же СВ может иметь положительную корреляцию по отношению к одной и в то же время – отрицательную, по отношению к другой.

32. Зависимости случайной величины и корреляции

Свойства коэффициента корреляции:

1 Если СВ независимы, то коэффициент корреляции = 0

2 Коэф-т корреляции изм-ся: 

3 Коэф-т корреляции хар-т не просто статистическую связь двух СВ, а только лин. Статистическую связь.

Y=aX, тогда коэф-т корреляции принимает следующие значения: rxy={+1, при а>0, 0, при а=0, -1, при а<0}

Такие функции записываются: rxy=sign(a)

4 Для нормального закона распределения: если СВ независим., то коэф-т корреляции=0 и , если коэф-т корреляции=0, то СВ независим.

33. Интервальные оценки

Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок. Пусть найденная по данным выборки статистическая хар-ка   служит оценкой неизвестного параметра . Будем считать  постоянным числом. Ясно, что  тем точнее определяет параметр , чем меньше абсолютная величина разности  , то чем меньше δ, тем оценка точнее. Т. о. положительное число δ характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка  удовлетворяет неравенству ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.

33. Понятие доверительной вероятности и доверительного интервала

Доверительной вероятностью оценки  по  называют вероятность γ, с которой осуществляется неравенство . Обычно надёжность оценки задаётся наперёд, причём в качестве γ берут число, близкое к единицы