Построение линейной регрессионной модели для условно однородной сети 10 кВ

Контрольная работа по курсу "Исследование и эксперимент в СЭС" для студентов заочной формы обучения

Задание:

Для условно однородной сети 10 кВ построить  линейную регрессионную модель  ∆Р=f(P₁, P₂), погрешность которой должна быть не более 1,0%  (считать  cosφ₁= cosφ₂ = 0,8 узловых нагрузок неизменными ).

Исходные данные:

Расчетная схема (по вариантам : а, б, в) приведена на рис. 1, а исходные данные по вариантам  задания - в табл. 1.

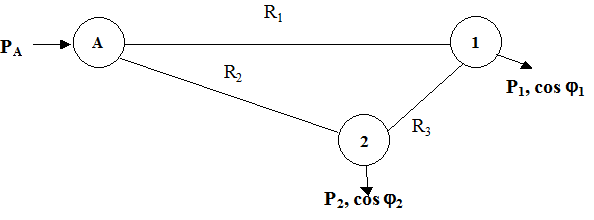         а) замкнутая схема («треугольник»)

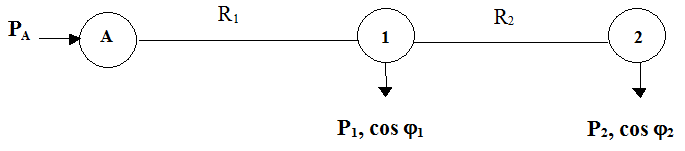
б) радиальная схема

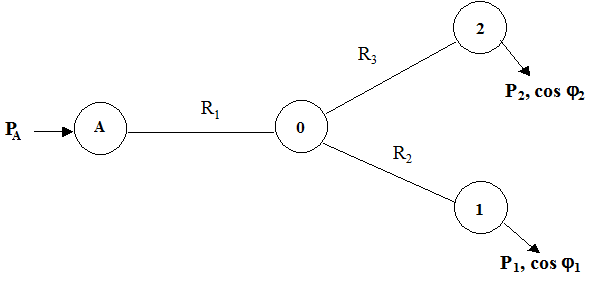
в)  схема в виде «звезды»

Рис.1. Расчетная схема (по вариантам: а, б, в )

Примечание: значения "Р" нагрузок узлов 1 и 2 могут изменяться в диапазоне ±20% от указанных значений, а значения "Q" определяются как    .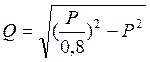

Таблица 1

Исходные данные по вариантам задания

Краткие методические указания :

Модель ∆Р=f(P₁, P₂) имеет 2 фактора и по условию задания требуется построить линейную модель, следовательно, она может иметь вид  ∆Р=b₀ + b₁∙P₁ + b₂∙P₂  или ∆Р=b₀ + b₁∙P₁ + b₂∙P₂ + b₁₂·P₁·P₂ .

Мощности Р₁ и Р₂ и их диапазоны изменения известны,  по условию косинусы нагрузок равны между собой и не меняются при изменении Р, т.е. остаются равными 0,8. В этом случае для любой Р реактивные нагрузки узлов определяются по известной формуле .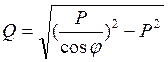

Поскольку заранее не известно, какая модель будет обеспечивать заданную точность, то сначала строят модель ∆Р=b₀ + b₁∙P₁ + b₂∙P₂ , и если она не обеспечивает заданную точность, то переходят к модели  ∆Р=b₀ + b₁∙P₁ + b₂∙P₂ + b₁₂·P₁·P₂ .  

“Имитационные” опыты (расчеты) выполняют в следующем порядке:

1) В соответствии с планом эксперимента и кодированным значением х_j

(табл. 2) определяют значение Р_j в натуральных единицах, т.е. Р_j=Р₀+x_j×dР; для каждого опыта, т.е. Р_j,1 и Р_j,2  (j=1, 2, 3,4 - номера опытов). Здесь P₀ – значение в середине диапазона изменения ( табл. 1), а dР=Р_макс-Р₀ ( или  dР=Р₀-Р_мин ) – диапазон изменения нагрузки относительно Р₀ . Максимальные и минимальные значения мощностей находятся как P_макс=Р₀+0.2∙P₀ ;  P_мин=Р₀-0.2∙Р₀ . Эти значения в кодированных значениях “x” соответственно равны (+1) и (-1).

2) Находят для каждого опыта реактивные нагрузки узлов в соответствии с принятыми  cos j1 = cos j2 = 0,8 т.е.:

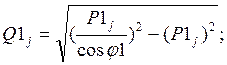
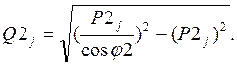    (j=1,2,3,4) .

3) Определяют потоки мощностей по ветвям схемы  и вычисляют суммарные потери активной мощности DР_j для всей сети в соответствии с полученными  P₁, P₂, Q1_j и Q2_j .