Электротехника \ Исследование и эксперимент в системах электроснабжения

Построение линейной регрессионной модели для условно однородной сети 10 кВ, страница 2

Все расчеты удобно оформлять в табличном виде, например, как это показано в  табл. 2.

Таблица 2

Информационная таблица

Номер

опыта

План

эксперимента

(матрица "x")

Значения активных мощностей нагрузок

Значения реактивных мощностей нагрузок

Суммарные потери активной мощности

j

xj,0

xj,1

xj,2

P1j

P2j

Q1j

Q2j

DРj

1

+1

-1

-1

2

+1

+1

-1

3

+1

-1

+1

4

+1

+1

+1

4) Коэффициенты уравнения регрессии   DP = bo+b1 ∙x1+b2 ∙x2  вычисляют обычным способом, т.е. или в матричном виде B=(xT ∙x)-1 ∙xT ∙DP  , или по простым формулам для ортогональной матрицы планирования: 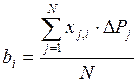     . Здесь N=4 – число опытов.

Уравнение регрессии приобретает вид  DP = bo+b1∙x1+b2∙x2 , в котором кодированные значения "x" изменяются в пределах от (–1) до (+1).

5) Так как параллельные опыты отсутствуют, то невозможно определить дисперсию всего эксперимента S2(y). В этом случае этой величиной или задаются, или определяют косвенно. В нашем случае известна (по условию), среднеквадратическая ошибка модели σм, не более 1%.  В центре эксперимента при х1=0 и х2=0 значение потерь определяет только один коэффициент b0.  В этом случае        S(y) = σм·b0 =  0.01·b0  и  тогда  S2(y) = (S(y))2 =(0.01·b0)2 .

6) Находят оценки дисперсий коэффициентов bi (i = 0, 1, 2) уравнения регрессии. Это можно сделать как в матричном виде для общего случая, т. е. вычисляя матрицу дисперсий-ковариаций  D = (xT×x)-1×S2(y) , так и по более простой формуле 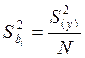  ,   (i = 0, 1, 2). Как видим, оценки дисперсий  коэффициентов для ортогонального плана (а у нас именно такой план) получаются  одинаковыми.

7) Проверяют адекватность линейного уравнения регрессии по критерию Фишера: 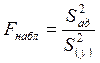,  где  ,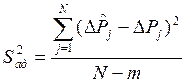

 расчетное ( ) и опытное значение потерь  для j-го опыта;   m - число коэффициентов модели (с учетом  bo).   Fкр=F0.05,n1, ,n2   (n1 = N-m=4-3=1 , n2 = N = 4 – число степеней свободы для числителя и знаменателя в формуле для  ).  Fкр также можно найти по таблицам [3]. Если Fнабл<Fкр  , то считается, что модель адекватно описывает опытные данные.

8) Если окажется, что линейная модель неадекватна, то она не может быть принята. В этом случае надо строить другую модель более сложную. В нашем случае можно ввести в линейную модель взаимодействие факторов типа х1х2, т.е. получить модель DP = bo+b1 ∙x1+b2 ∙х2 + b12· x1· x2 .  Для этого достаточно рассчитать еще один коэффициент b12 по формуле: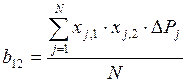 

В дальнейшем все последующие пункты выполняют применительно уже к модели с взаимодействием.

9) Проверяют значимость коэффициентов уравнения регрессии по условию   

| bi | і tкрЧSbi, где  tкр=t0.05, N=t0.05, 4 определяется по таблицам Стьюдента [3], а    - средние квадратичные ошибки коэффициентов bi.

Незначимые коэффициенты отбрасываются и получается, так называемая, "усеченная" модель. В этом случае желательно еще раз проверить на адекватность и "усеченную" модель.

10) Для перехода от уравнения регрессии  y = DP = bo+b1∙x1+b2∙x2 в кодированных значениях "x"  к  уравнению  DP = bo+b1∙P1+b2∙P2 в натуральных значениях "P" достаточно заменить  в уравнении регрессии "x" на x=(P-P0)/ dP для каждого фактора (где Р0 и dP – конкретные числа) . Здесь уже значения "Р" изменяются в своих заданных пределах.

11) С помощью модели ∆Р=f(P1, P2) выполнить анализ потерь активной мощности. Для этого на одном графике в зависимости от номеров опытов j построить  и  и оценить в % их максимальное расхождение. Выявить изменение какой из нагрузок больше влияет на потери.

12) Для наглядности можно построить зависимости   DP = f(P2), например, для трех фиксированных значений  Р1=Р1 мин; Р1=Р1 0; Р1=Р1 макс .   То же самое можно сделать и для DP = f(P1) при Р2=Р2 мин; Р2=Р2 0; Р2=Р2 макс .  Большую наглядность имеет трехмерный график  ∆Р=f(P1, P2), построенный в виде поверхности в зависимости от Р1 и Р2, однако его можно построить только с помощью какого-либо математического пакета, например, такого как MathCad, MatLab и т.д.

Примечание:контрольную работу можно выполнять как вручную  без использования ПК, так и  с использованием ПК (в этом случае удобно использовать  математический  пакет MathCad).

Литература для выполнения контрольной работы

1.  Ф.Г. Гусейнов, О.С. Мамедяров. Планирование эксперимента в задачах электроэнергетики. -М.:  Энергоатомиздат, 1988. -151 с.

2.  Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. Планирование эксперимента при поиске оптимальных условий. -М.:. «Наука», 1978. -279 с. 

3. Гмурман В. Е. Руководство к  решению задач по теории вероятностей и математической статистике.  -М.:  «Высш. школа», 1979. -400 с.

Скачать файл