Решение задачи Коши для системы обыкновенных дифференциальных уравнений

Отчет

По практической работе №4

«Решение задачи Коши для СОДУ»

Калюхович Юрий, 319 гр.

Санкт-Петербургский государственный университет

1. Содержание задания.

1) Используя условия порядка для двухэтапного явного метода Рунге-Кутты второго порядка построить рассчетную схему второго порядка при значении

2) Построить и программно реализовать алгоритм решения задачи Коши

 ,    

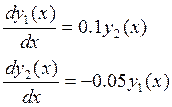с точностью  по полной погрешности и оценкой по методу Рунге (на базе полученной рассчетной схемы и схемы-оппонента).

3) Построить и программно реализовать алгоритм решения задачи Коши с автоматическим выбором шага с заданной максимально допустимой локальной погрешностью  и оценкой по методу Рунге (на базе полученной рассчетной схемы и схемы-оппонента).

2. Теоретические основы.

Необходимо найти решение 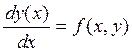, удовлетворяющее начальным условиям . Будем рассматривать дискретные методы решения данной задачи, т.е. вычисляется последовательность приближений на множестве точек , h – шаг сетки. Рассмотрим явные одношаговые методы Рунге-Кутты:

Если использовать для поиска решения разложение в ряд Тейлора, ограничиваясь конечным числом членов ряда, то можно записать:

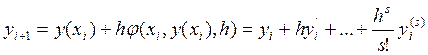, производные  могут быть найдены из . Так, для s=1 получим явный метод Эйлера:

.

По таким формулам уже можно последовательно получать приближенные решения .

Явные методы Рунге-Кутты основаны на построении функции , максимально близкой к , и не содержит производных правой части. Общая схема:

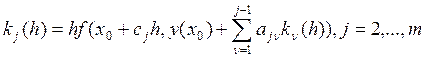
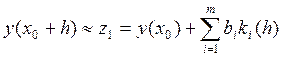
- m-этапный явный метод Рунге-Кутты (ЯМРК) для задачи Коши.

Применяемая в нашей задаче рассчетная схема 4-го порядка называется правилом одной шестой (Классический метод Рунге-Кутты)

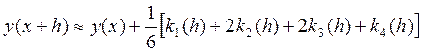, где

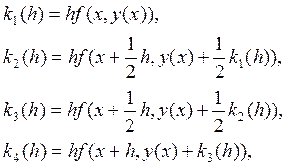
Согласно правилу Рунге, для оценки глобальной погрешности при вычислении с постоянным шагом необходимо провести вычисления с данным шагом и с вдвое меньшим, при этом получим 2 приближенных решения  и  . Тогда для каждого из них можно вычислить глобальную погрешность:

,       .

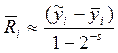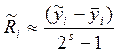Оптимальную длину шага можно определить: .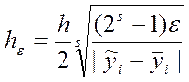

Для определения локальной погрешности при вычислении с переменным шагом необходимо сделать 1 шаг длины h, и на том же отрезке 2 шага длиной h/2 каждый. Тогда представление для главного члена погрешности на шаге h:

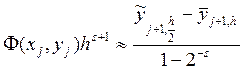
3. Реализация

файл code.cpp:

#include "defs.h"

/**

* solution from Maple: {y1(Pi) = 0.2511060625, y2(Pi) = 0.2819679454}

**/

int main(int argc, char argv[])

{

//precision of output:

int zu=10;

cout.precision(zu);

//start conditions:

long double y0[2];

y0[0] = 0.05*Pi;

y0[1] = 0.1*Pi;

//variables:

long double y[2];

long double y2[2];

//calculate a first step:

long double delta = pow(Pi, -3) + pow(Pi*sqrt(17.0)/400, 3);

long double dx = pow(e/delta, (long double)1.0/3);

//with my method:-----------------------------------------------------------------------cout << "-----my method-----\n";

for(int i=0; i<=Pi/dx; i++)

{

//dx=

y[0] = my_method(y0[0], y0[1], dx, 0.1);

y[1] = my_method(y0[1], y0[0], dx, -0.05);

y0[0] = y[0];

y0[1] = y[1];

}

y[0] = my_method(y0[0], y0[1], Pi - (int)(Pi/dx) * dx, 0.1);

y[1] = my_method(y0[1], y0[0], Pi - (int)(Pi/dx) * dx, -0.05);

y0[0] = 0.05*Pi; y0[1] = 0.1*Pi;

for(int i=0; i<=Pi/dx; i++)

{

y2[0] = my_method(y0[0], y0[1], 0.5*dx, 0.1);

y2[1] = my_method(y0[1], y0[0], 0.5*dx, -0.05);

y0[0] = y2[0];

y0[1] = y2[1];

}

y2[0] = my_method(y0[0], y0[1], 0.5*(Pi - (int)(Pi/dx) * dx), 0.1);

y2[1] = my_method(y0[1], y0[0], 0.5*(Pi - (int)(Pi/dx) * dx), -0.05);

if((abs(1.0*(y2[0]-y[0])/7) > e) && (abs(1.0*(y2[1]-y[1])/7) > e))

{

cout << "accuracy is not received..:( =->" << endl;

}

cout << "mine: " << y2[0] << '\t' << y2[1] << endl;

cout << "accuracy: y[0]: " << abs(1.0*(y2[0]-y[0])/3) << "  y[1]: " << abs(1.0*(y2[1]-y[1])/3) << endl;

cout << "with optimized step:\n";

dx = 0.5*dx*sqrt((e*3)/sqrt((y2[0]-y[0])*(y2[0]-y[0]) + (y2[1]-y[1])*(y2[1]-y[1])));

const long double optimal = dx;

y0[0] = 0.05*Pi; y0[1] = 0.1*Pi;

for(int i=0; i<=Pi/dx; i++)

{

y2[0] = my_method(y0[0], y0[1], dx, 0.1);

y2[1] = my_method(y0[1], y0[0], dx, -0.05);

y0[0] = y2[0];

y0[1] = y2[1];

}

y2[0] = my_method(y0[0], y0[1], 0.5*(Pi - (int)(Pi/dx) * dx), 0.1);

y2[1] = my_method(y0[1], y0[0], 0.5*(Pi - (int)(Pi/dx) * dx), -0.05);

cout << "mine_optimized: " << y2[0] << '\t' << y2[1] << endl;

//with opposed method:----------------------------------------------------------------------------------cout << "\n-----opposed method-----\n";

y0[0] = 0.05*Pi;

y0[1] = 0.1*Pi;

for(int i=0; i<=Pi/dx; i++)

{

y[0] = opposed_method(y0[0], y0[1], dx, 0.1);

y[1] = opposed_method(y0[1], y0[0], dx, -0.05);

y0[0] = y[0];

y0[1] = y[1];

}

y0[0] = 0.05*Pi;

y0[1] = 0.1*Pi;

for(int i=0; i<=Pi/dx; i++)

{

y2[0] = opposed_method(y0[0], y0[1], 0.5*dx, 0.1);

y2[1] = opposed_method(y0[1], y0[0], 0.5*dx, -0.05);

y0[0] = y2[0];

y0[1] = y2[1];

}

if(abs(1.0*(y2[0]-y[0])/63) > e && abs(1.0*(y2[1]-y[1])/63) > e)

{

cout << "accuracy is not received..:(" << endl;

}

cout << "opposed: " << y2[0] << '\t' << y2[1] << endl;

cout << "accuracy: y[0]: " << abs(1.0*(y2[0]-y[0])/15) << "  y[1]: " << abs(1.0*(y2[1]-y[1])/15) << endl;

cout << "with optimized step:\n";

dx = 0.5*dx*sqrt((e*15)/sqrt((y2[0]-y[0])*(y2[0]-y[0]) + (y2[1]-y[1])*(y2[1]-y[1])));

y0[0] = 0.05*Pi;

y0[1] = 0.1*Pi;

for(int i=0; i<=Pi/dx; i++)

{

y2[0] = opposed_method(y0[0], y0[1], dx, 0.1);

y2[1] = opposed_method(y0[1], y0[0], dx, -0.05);

y0[0] = y2[0];

y0[1] = y2[1];

}

y2[0] = opposed_method(y0[0], y0[1], 0.5*(Pi - (int)(Pi/dx) * dx), 0.1);