Регрессионный анализ исходных данных о тестах IQ, опыте работы и индексе эффективности 30 сотрудников компании Joseph Machine Company. Прогноз и исследование динамики объема продаж, страница 4

Анализ временных рядов находит широкое применение в экономике при изучении динамики предпринимательской деятельности и прогнозировании будущих значений таких важнейших показателей, как , например, объем продаж, ставки процента и т.д.

Рассмотрим производителя мороженого фирму Ice-cream , которая заинтересована в прогнозе и исследовании динамики объема продаж.

Проверим исходный временной ряд на наличие детерминированных составляющих. Для этого воспользуемся критерием серий, основанным на медиане выборки. Сравнивая каждое значение выборки с медианой, получается последовательность серий с параметрами: количество серий и длина максимальной серии . На основании этих параметров гипотеза о случайности отвергается, т.е. во временном ряде присутствует неслучайная компонента. Построим диаграмму ряда.

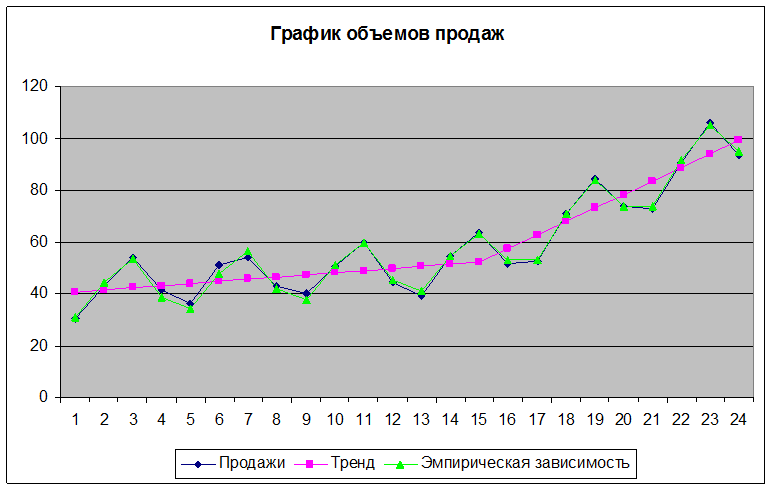
На графике видно, что линейный тренд не был постоянным, а точка изгиба находится примерно на отрезке [14; 16]. Таким образом общее уравнение парной линейной регрессии имеет следующий вид.

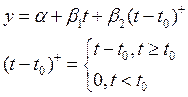
Для каждого  построим регрессионную модель и проверим гипотезу Дарбина-Уотсона.

Таким образом, оптимальное значение  равно 15. Уравнение парной линейной регрессии в этом случае имеет следующий вид.

График тренда приведен на диаграмме выше.

Теперь можно оценить сезонную составляющую с периодом равным году. В данном случае получается 6 периодов, длительность каждого из которых равна 4.

Построим эмпирическую. Ее график приведен на диаграмме выше. Вычислив остатки, проверим гипотезы случайности и Дарбина-Уотсона. Обе гипотезы принимаются, поэтому можно сделать вывод о том, что построенная регрессионная модель является адекватной.

Учитывая адекватность модели, можно воспользоваться ей для прогнозирования объема продаж на четыре квартала 2004 года.