Регрессионный анализ находит широкое применение в маркетинговых исследованиях, когда изучается взаимосвязь двух и более переменных. Рассмотрим изготовителя шариковых ручек Click, который заинтересован в исследовании эффективности маркетинговых усилий своей фирмы. Компания использует оптовых торговцев для реализации продукции Click и в дополнение к их усилиям прибегает к персональным продажам и коротким рекламным телероликам. Компания планирует использовать в качестве меры оценки эффективности ежегодный объем продаж по территориям. ( Г.А. Черчилль «Маркетинговые исследования»)
|
Территория |
Продажа (тыс. долларов)
|
Телевизионная реклама (число показов в месяц) |
Число торговых представителей
|
|
005 019 033 039 061 082 091 101 115 118 133 149 162 164 178 187 189 205 222 237 242 251 260 266 279 298 306 332 347 358 |
263,9 283,5 277,8 415,1 432,6 317,8 568,7 576,8 424,8 313,9 405,2 223,0 341,8 648,5 520,4 329,5 426,0 341,8 451,9 425,8 241,1 503,9 372,3 265,5 620,9 450,5 270,5 368,0 556,1 570,0 |
6 8 6 10 13 7 13 17 13 7 11 5 9 17 19 9 11 8 13 14 7 16 8 5 19 18 4 7 12 13 |
2 4 3 4 5 4 6 7 3 4 6 4 4 8 7 3 6 2 5 5 4 6 5 3 5 5 3 6 7 6 |
Парные линейные регрессии
Построим парную
линейную регрессию показателя ![]() на
каждый из факторов
на
каждый из факторов ![]() и
и ![]() . Уравнения регрессий имеют
следующий вид.
. Уравнения регрессий имеют
следующий вид.
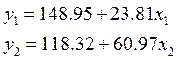
|
Фактор |
Фактор |
|
|
t-статистика коэффициента а |
5.20365 |
2.61169 |
|
t-статистика коэффициента b |
9.71981 |
6.69245 |
|
F-статистика |
94.4746 |
44.7888 |
|
F табличное |
4.19597 |
|
|
t табличное |
2.04841 |
|
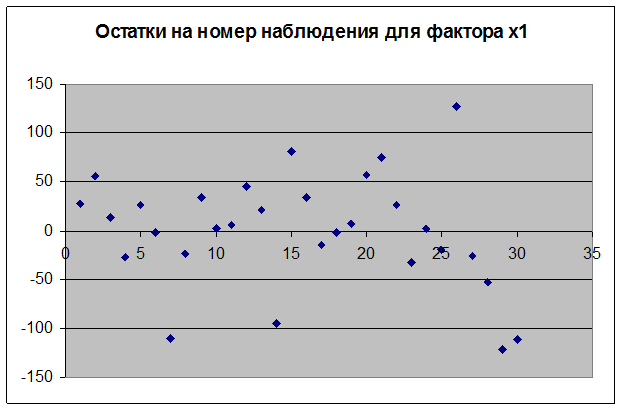
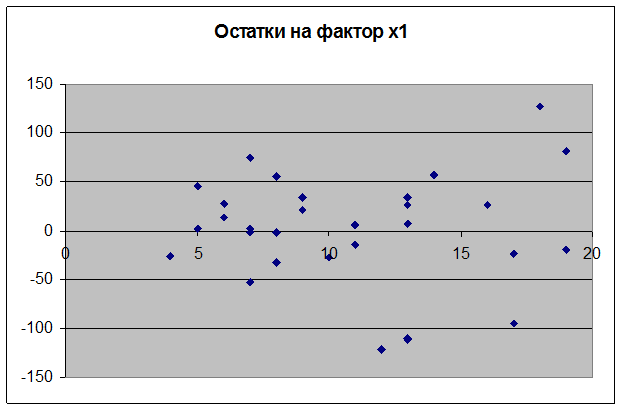
Коэффициенты a и b являются статистически значимыми. Обе модели регрессии также являются статистически значимыми. Это означает, что продажи зависят как от телевизионной рекламы, так и от числа торговых представителей.


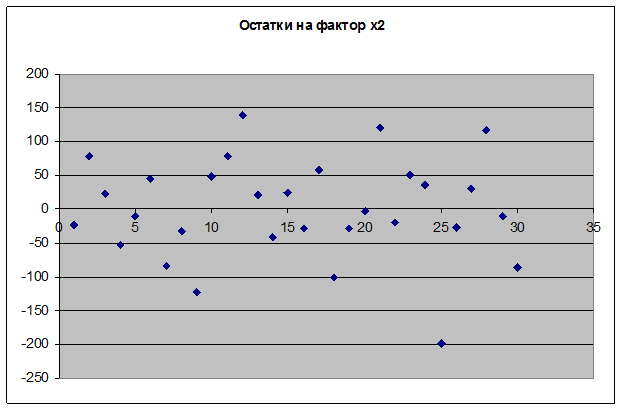
Множественная линейная регрессия
Уравнение множественной линейной регрессии имеет следующий вид.
![]()
|
t-статистика коэффициента a |
2.96024 |
|
t-статистика коэффициента b1 |
6.08374 |
|
t-статистика коэффициента b2 |
3.32316 |
|
F статситискика |
69.7027 |
|
t табличное |
2.05183 |
|
F табличное |
3.35413 |
На основе t и F статистик можно сделать вывод о том, что коэффициенты и модель в целом являются статистически значимыми.
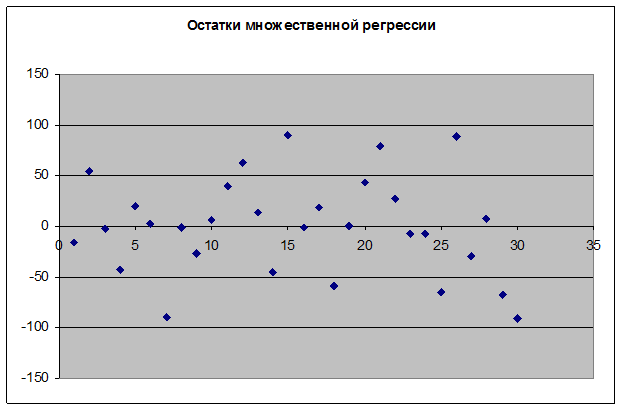
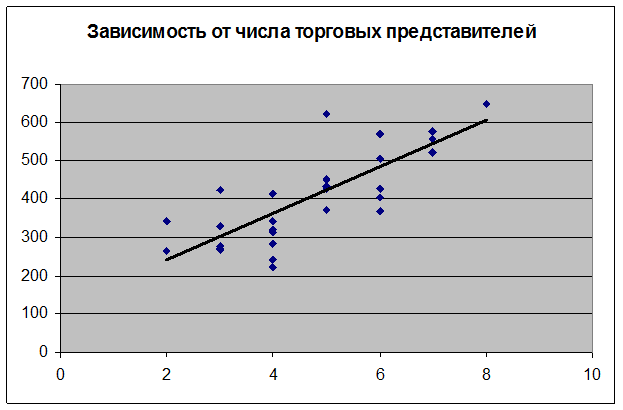
Из диаграммы видно, что уравнение множественной линейной регрессии лучше моделирует исходные данные. Следовательно, лучше учитывать оба фактора вместе.
Прогноз показателя
Построим прогноз объемов продаж для значений факторов на 235% превышающих средние значения факторов, используя парные и множественную регрессии.
|
Фактор
|
Фактор |
|
|
Среднее значение |
10.83 |
4.73 |
|
Значение фактора |
36.30 |
15.86 |
|
Значение прогноза |
1013.16 |
1085.11 |
|
Ошибка точечного прогноза |
60.18 |
77.82 |
|
Доверительный интервал |
889.90 |
925.69 |
|
1136.42 |
1244.52 |
|
|
Прогноз с помощью множественной линейной регрессии |
1152.19 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.