Исследование зависимости объема продаж от числа показов рекламы в месяц/от числа торговых представителей (на примере изготовителя шариковых ручек Click)

Санкт-Петербургский государственный университет

Факультет прикладной математики – процессов управления

МЕТОДЫ СТАТ. ОБРАБОТКИ ИНФОРМАЦИИ

Задание 2.4

Преподаватель:  Буре В.М.

Выполнила: Салахиева Марина

Санкт-Петербург

2010

Тест 2.4

Регрессионный анализ находит широкое применение в маркетинговых исследованиях, когда изучается взаимосвязь двух и более переменных. Рассмотрим изготовителя шариковых ручек Click, который заинтересован в исследовании эффективности маркетинговых усилий своей фирмы. Компания использует оптовых торговцев для реализации продукции Click и в дополнение к их усилиям прибегает к персональным продажам и коротким рекламным телероликам. Компания планирует использовать в качестве меры оценки эффективности ежегодный объем продаж по территориям. ( Г.А. Черчилль «Маркетинговые исследования»)

Территория	Продажа (тыс. долларов)	Телевизионная реклама (число показов в месяц)	Число торговых представителей
005 019 033 039 061 082 091 101 115 118 133 149 162 164 178 187 189 205 222 237 242 251 260 266 279 298 306 332 347 358	270,9 282,8 269,0 415,8 437,5 316,9 563,9 574,8 421,8 316,3 405,4 224,0 348,6 643,2 525,4 320,5 424,8 344,0 451,4 423,8 245,1 502,3 372,3 267,1 625,6 452,5 275,1 362,0 556,8 571,0	5 8 7 10 12 7 11 16 13 5 10 5 9 19 20 10 12 7 14 14 2 16 9 4 18 18 4 8 11 13	4 6 2 5 8 4 7 9 4 2 6 5 4 8 6 3 5 3 4 5 4 7 5 3 6 5 3 6 6 6

1. Рассмотрим зависимость объема продаж от числа показов рекламы в месяц:

Уравнение линейной регрессии: y(x1) = 182.0332 + 21.292125^.x1

коэффициент корреляции   r_xy = 0.8576

коэффициент детерминации  R² = 0.7355

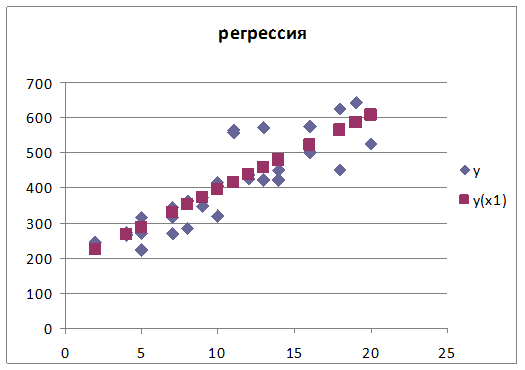
Построенное уравнение линейной регрессии статистически значимо т.к. F = 77.859 а критическая точка по таблице распределения Фишера 4,1959. Следовательно, существует линейной зависимости между объемом продаж и  числом показов рекламы в месяц, причем связь достаточно высокая (коэффициент детерминации ).

Пользуемся критерием Жарка-Бера для проверки гипотезы о нормальном распределении остатков, коэффициент JB = 2.9209 значение по таблице распределения χ² примерно 5.99. Сравнив значения, делаем  вывод, что остатки подчиняются нормальному закону распределения.

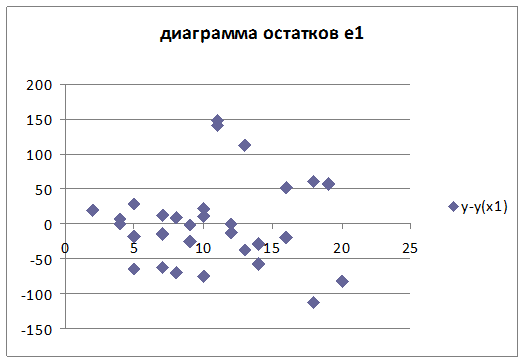
Проверяем статистическую значимость коэффициентов a и b:

Стандартные ошибки параметров регрессии, соответствующие значения t-статистик:

m_a =  27.964

m_b  =2.413

ta=6.5095,

tb=8.8237,

t_крит=2.0484.

После сравнения данных статистик, приходим к тому, что коэффициенты  а и b статистически значимы.

Доверительные интервалы и прогноз:

124.7511 ≤ α ≤ 239.3153 

16.34924 ≤ β ≤ 26.23501

При XP =29.058 Yp=800.7469 или можно рассмотреть оценку 669.75 ≤ Yp ≤ 931.7436.

Вывод: Согласно построенной модели регрессии между выручкой от продаж и  числом показов рекламы в месяц существует линейная зависимость, причем связь достаточно высокая (коэффициент детерминации ). 

2. Рассмотрим зависимость объема продаж от числа торговых представителей:

Уравнение линейной регрессии: y(x2) = 159.69+49.1384^.х2

коэффициент корреляции   r_xy = 0.71623

коэффициент детерминации  R² = 0.513

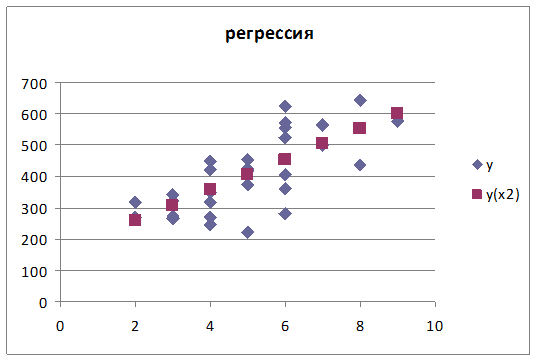
Построенное уравнение линейной регрессии статистически значимо т.к. F = 29.4936 а критическая точка по таблице распределения Фишера 4,1959. Следовательно, существует линейная зависимость между объемом продаж и  числом показов рекламы в месяц, причем связь достаточно высокая (коэффициент детерминации ).

Пользуемся критерием Жарка-Бера для проверки гипотезы о нормальном распределении остатков, коэффициент JB = 0.53836 значение по таблице распределения χ² примерно 5.99. Сравнив значения, делаем  вывод, что остатки подчиняются нормальному закону распределения.

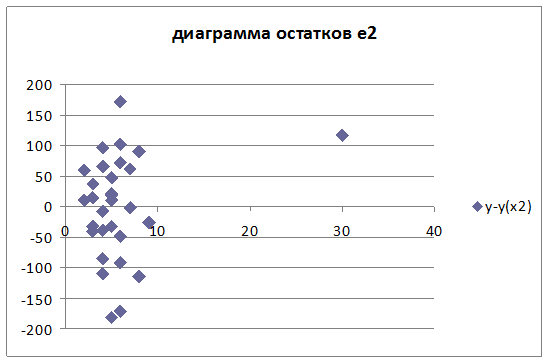
Проверяем статистическую значимость коэффициентов a и b:

Стандартные ошибки параметров регрессии, соответствующие значения t-статистик:

m_a =  48.134

m_b  =9.0481

ta=3.31763,

tb=5.4308,

t_крит=2.0484.

После сравнения данных статистик, приходим к тому, что коэффициенты  а и b статистически значимы.

Доверительные интервалы и прогноз:

61.09 ≤ α ≤ 258.287 

30.604 ≤ β ≤ 67.67

При XP =13.8416 Yp=839.847 или можно рассмотреть оценку 661.8033 ≤ Yp ≤ 1017.8916.

Вывод: Согласно построенной модели регрессии между выручкой от продаж и  числом показов рекламы в месяц существует линейная зависимость, причем связь достаточно высокая (коэффициент детерминации ). 

3. Построим множественную регрессию показателя на все факторы и проверим статистическую значимость коэффициентов и уравнения в целом.

Уравнение множественной регрессии имеет следующий вид:

y(x) = 127,289 +16,68^.x1+20,56^.x2

Коэффициент детерминации R²=0,7907

Посчитаем статистику F=51.0281. После сравнения ее с критическим значением Fтабл = 3,3541, делаем вывод:  построенное уравнение множественной регрессии статистически значимо.

Пользуемся критерием Жарка-Бера для проверки гипотезы о нормальном распределении остатков, коэффициент JB = 1.3596 значение по таблице распределения χ² примерно 5.99. Сравнив значения, делаем  вывод, что остатки подчиняются нормальному закону распределения.

Проверяем статистическую значимость коэффициентов a,b1,b2:

ta=3,907,

tb1=5,988,

tb2=2,67,

t_крит=2.05.

Из сравнения данных статистик видно, что коэффициенты