Минимизация квадратичных функций. Градиентный метод наискорейшего спуска для отыскания минимума квадратичной функции f(x)=1\2+, страница 3

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №8

1.  Изложить l – шаговый стационарный оптимальный градиентный метод спуска для отыскания минимума квадратичной функции ([5, 472, 475]):

                                                                f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица: . Указать скорость сходимости и оценку погрешности.

2.  Реализовать на компьютере для l=2 с критерием остановки: <e, e - заданная точность приближенного решения.

Продемонстрировать работу программы для

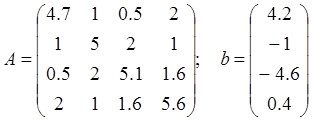
Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, e, m, M. Как известно, , где - наибольшее и наименьшее собственные значения матрицы А. Для нахождения m и М использовать следующие две оценки:  где .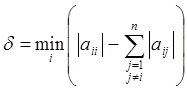

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №9

1.  Изложить l – шаговый стационарный оптимальный градиентный метод спуска для отыскания минимума квадратичной функции ([5, 472, 475]):

                                                                f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица: . Указать скорость сходимости и оценку погрешности.

2.  Реализовать на компьютере для l=3 с критерием остановки: <e, e - заданная точность приближенного решения.

Продемонстрировать работу программы для

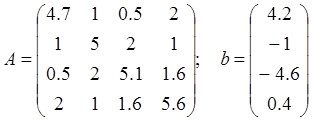
Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, e, m, M. Как известно, , где - наибольшее и наименьшее собственные значения матрицы А. Для нахождения m и М использовать следующие две оценки:  где .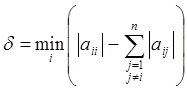

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №10

1.  Изложить градиентный метод наискорейшего спуска (ГМНС) для отыскания минимума квадратичной функции ([3, 52-53, 59-61], [5, 456-465]):

f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица: . Указать скорость его сходимости и связь с решением системы уравнений Ах+b=0.

2.  Реализовать ГМНС на компьютере. В качестве критерия прекращения спуска: <e, где х^* - точка минимума f(x), e - заданная точность приближенного решения.

Продемонстрировать работу программы для

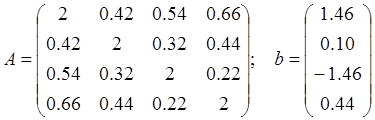
Границы m и M матрицы А, необходимые для оценки погрешности метода, найти, используя следующие два неравенства:

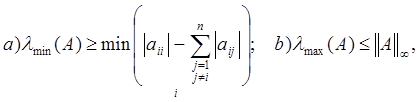 где - наибольшее и наименьшее собственные значения матрицы А.

Литература.

1.  Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988