Минимизация квадратичных функций. Градиентный метод наискорейшего спуска для отыскания минимума квадратичной функции f(x)=1\2+, страница 2

Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, e, . Решить систему и сравнить  с . Проверить вычисления при различных начальных векторах  и проследить за зависимостью k от .

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №5

1.  Изложить метод сопряженных градиентов (МСГ) для отыскания минимума квадратичной функции ([1, 73-82, метод Флетчера-Ривеа]):

                                                                f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица, <*,*> - скалярное произведение в Rⁿ. Каково основное свойство МГС?

2.  Реализовать МСГ на компьютере. Критерий прекращения спуска:

Продемонстрировать работу программы для

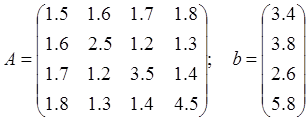
Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, .

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №6

1.  Изложить l – шаговый метод наискорейшего спуска для отыскания минимума квадратичной функции ([5, 472, 475]):

                                                                f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица, <*,*> - скалярное произведение в Rⁿ.

2.  Реализовать на компьютере l=2. В качестве критерия прекращения спуска предусмотреть                         любой из трех следующих:

Продемонстрировать работу программы для

Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, e, . Решить систему и сравнить  с . Проверить вычисления при различных начальных векторах  и проследить за зависимостью k от .

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978

2.  Васильев Ф. П.  Численные методы решения экстремальных задач, М. 1988

3.  Пшеничный Б.Н., Данилин  Ю. М. Численные методы в экстремальных задачах, М. 1975

4.  Карманов В. Г. Математическое программирование, М., 1986 (176-180, 203-205) и М.1980 (170—174, 195-197)

5.  Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры, М.1960

Минимизация квадратичных функций.

Задание №7

1.  Изложить l – шаговый метод наискорейшего спуска для отыскания минимума квадратичной функции ([5, 472, 475]):

                                                                f(x)=1\2<Ax,x>+<b,x>,                      (1)

где – симметричная положительно определенная матрица, <*,*> - скалярное произведение в Rⁿ.

2.  Реализовать на компьютере l=2. В качестве критерия прекращения спуска предусмотреть                         любой из трех следующих:

Продемонстрировать работу программы для

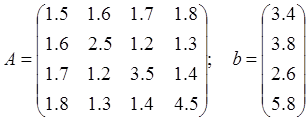
Выходные данные программы:  - номер последнего шага, входные данные: n, A, b, e, . Решить систему и сравнить  с . Проверить вычисления при различных начальных векторах  и проследить за зависимостью k от .

Литература.

1. Моисеев Н. Н., Иванилов Ю.П., Сталярова Е. М. Методы оптимизации, М. 1978