Интерполирование функций. Интерполирование функции с наименьшими вычислительными затратами

Практикум по методам вычислений

ОТЧЁТ ПО ТЕМЕ 5:

Интерполирование функций

Студент:

Марковнин П.В., 319 гр.

Преподаватель:

Остов Ю.Я.

факультет ПМ-ПУ   СПбГУ   2007

Задача интерполирования состоит в построении интерполяционных полиномов Лагранжа по формуле 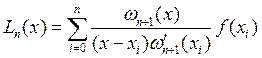 с использованием узлов , , …, , выбранных на отрезке непрерывности данной функции.

В данном случае построение интерполяционного полинома идёт для функции

F(x) = x²-sin10x:

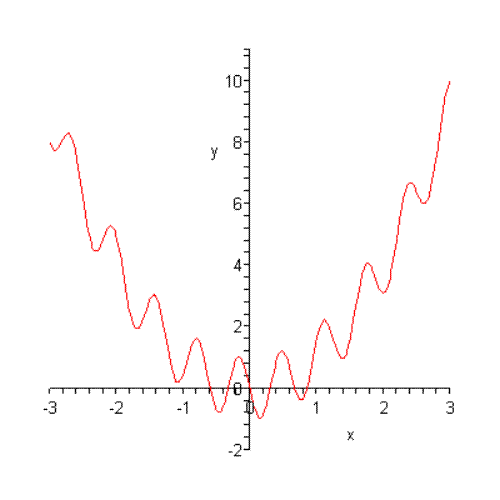
Рассмотрим интервал непрерывности [2.8, 3] и проделаем для него процедуру интерполирования, выбирая сперва равноотстоящие узлы, а потом такое же количество точек, но в соответствии с формулой 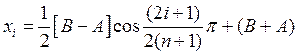, где , а А и В – границы промежутка непрерывности.

//--------------------------------------------------------------------------#pragma hdrstop

#include <iostream>

#include <cmath>

//--------------------------------------------------------------------------#pragma argsused

using namespace std;

// исходная функция

double func(double x)

{

return x*x - sin(10*x);

}

// узлы по формуле (6)

double fixedNodes(int i, int n, double A, double B)

{

return 0.5*((B - A)*cos((2*i + 1)*3.14/(2*(n + 1))) + B + A);

}

// общая формула для вычисления множителя Ланранжа

double l(double x, double nds[], int k, int n)

{

double res = 1;

for(int i = 0; i <= n; i ++)

{

if(i != k)

{

res *= (x - nds[i])/(nds[k] - nds[i]);

}

}

return res;

}

// вычисление полинома Лагранжа

double L(double x, double nds[], int n)

{

double res = 0;

for(int i = 0; i <= n; i ++)

{

res += l(x, nds, i, n)*func(nds[i]);

}

return res;

}

int main()

{

int n,

N = 20;

double A = 2.8,

B = 3,

Xk = A,

h,

nodes[100],

nodes_fixed[100],

nodes_100[200];

cout<<"Vvedite n: ";

cin>>n;

h = (B - A)/n;

cout<<endl<<"Ravnootstoyaschie yzlu:"<<endl;

// массив с равноотстоящими узлами

for(int i = 0; i <= n; i ++)

{

nodes[i] = Xk; 

cout<<nodes[i]<<" ";

Xk += h;

}

// массив с узлами, полученными по формуле (6)

cout<<endl<<endl<<"Yzlu, polychennue po formyle:"<<endl;

for(int i = 0; i <= n; i ++)

{

nodes_fixed[i] = 0.5*((B - A)*cos(3.14*(2*i + 1)/(2*n + 2)) + A + B);

cout<<nodes_fixed[i]<<" ";

} 

// значения функции и полинома в равноотстоящих узлах

cout<<endl<<endl<<"Znacheniya f(x) i L(x) v ravnootstoyaschih yzlah:"<<endl;

for(int i = 0; i <= n; i ++)

{

cout<<nodes[i]<<" "<<func(nodes[i])<<" "<<L(nodes[i], nodes, n)<<endl;

} 

// значения функции и полинома в узлах, полученных по формуле (6)

cout<<endl<<"Znacheniya f(x) i L(x) v yzlah, polychennuh po formyle:"<<endl;

for(int i = 0; i <= n; i ++)

{

cout<<nodes_fixed[i]<<" "<<func(nodes_fixed[i])<<" "<<L(nodes_fixed[i], nodes_fixed, n)<<endl;

}

// проверим поведение полинома в других точках указанного интервала

cout<<endl<<endl<<"Vvedite N >> n: ";

cin>>N;

h = (B - A)/N;

Xk = A;

/* значения функции и полинома в других точках интервала [A; B]; значения функции и полинома должны совпадать в тех точках, значение которых совпадает с одним из узлов   */

cout<<endl<<endl<<"Znacheniya f(x) i L(x) na proizvolnuh tochkah intervala ["<<A<<"; "<<B<<"]: "<<endl;

for(int i = 0; i <= N; i ++)

{

cout<<Xk<<" "<<func(Xk)<<" "<<L(Xk, nodes, n);

if(func(Xk) == L(Xk, nodes, n)) cout<<" *";

cout<<endl;

Xk += h;

}

cout<<endl;  

system("pause");

return 0;

}

//--------------------------------------------------------------------------Результаты листинга с использованием трёх узлов интерполирования:

Vvedite n: 3

строим равноотстоящие узлы:

2.8 2.86667 2.93333 3

узлы, полученные методом Чебышева:

2.9924 2.93832 2.86182 2.80767

значения функции и полинома в равноотстоящих узлах:

2.8 7.56909 7.56909

2.86667 8.60012 8.60012

2.93333 9.47631 9.47631

3 9.98803 9.98803

Значения функции и полинома в узлах, полученных методом Чебышева

2.9924 9.95133 9.95133

2.93832 9.52895 9.52895