Решение систем линейных алгебраических уравнений. Метод простых итераций (схема метода, условия сходимости и оценка погрешности) для решения системы

Санкт-Петербургский Государственный Университет

Факультет Прикладной математики – Процессов Управления

Отчет по методам вычисления

Задание 17

Решение систем линейных алгебраических уравнений

Выполнил: Каганова Екатерина

Группа: 212

Проверил:_______________

     Оценка:_________________

2005

Содержание

1.  Условие задач……………………………………...стр.3

2.  Задание 1……………………………………………стр.4-5

3.  Задание 2……………………………………………стр.6-7

4.  Задание 3……………………………………………стр.8

5.  Список литературы…………………………...…..стр.9

Условие задач

1. Как влияют на решение систем линейных алгебраических уравнений  Ax=C (1)  с квадратной не вырожденной матрицей А погрешности задания этой матрицы и вектора С, а так же погрешности арифметических операций, возникающих при реализации какого-нибудь точного метода решения системы (1) на ЭВМ?

2. Изложить теоретические основы метода простых итераций (схему метода, условия сходимости и оценку погрешности) для решения системы (1). Указать типы матриц A, для которых условия сходимости можно проверить.

3. Составить и отладить программу, реализующую указанный  в задании 2 метод с требуемой точностью. Продемонстрировать ее работу на примере системы (1) с

A=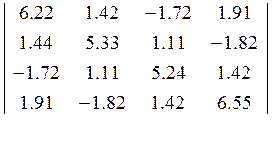  

C=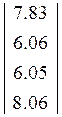

Задание 1

Как влияют на решение систем линейных алгебраических уравнений  Ax=C (1)  с квадратной не вырожденной матрицей А погрешности задания этой матрицы и вектора С, а так же погрешности арифметических операций, возникающих при реализации какого-нибудь точного метода решения системы (1) на ЭВМ?

Будем считать, что относительно матрицы A и столбца c нам известно, что:

,

,

где  - приближенные значения матриц А и с, а  и  - оценки абсолютных погрешностей задания их элементов.

Тогда рассмотрим систему , где  удовлетворяют неравенствам выше.

Невозмущенным решением задачи Ах=с будем называть вектор-столбец , удовлетворяющий системе:

,

,

а возмущенным решением - любое решение системы .

Рассмотрим, как сильно могут отличаться возмущенные решения от невозмущенного решения .

Рассмотрим систему уравнений  и возмущенную систему , где , , - погрешности величин А, c, . При этом считаем, что det, для всех :.

Вычитая равенства получаем:        ,    и

Оценивая по норме погрешность  получаем:

Считая, что  получим оценку:

Часто погрешность матрицы Ах=с многоменьше погрешности правой части, поэтому рассмотрим случай =0, тогда из последнего неравенства получим:

,

так как , то для  имеем оценку:

.

С учетом этой оценки, последнее неравенство записывается следующим образом: .

- мера обусловленности матрицы . Если она много больше 1, то решение x системы Ах=с может сильно отличаться от невозмущенного решения . Такие системы называют плохо обусловленными.

При реализации какого-либо метода решения систем линейных уравнений на ЭВМ мы можем столкнуться с проблемой вычислительной погрешности, если на ЭВМ существует ограничение на порядки чисел, или к этому приводит небольшая разрядность чисел в ЭВМ. В итоге случается недопустимое искажение результата вычислительной погрешности.

Полная погрешность является суммой погрешности метода и вычислительной погрешности. Вычислительная погрешность складывается из неустранимой погрешности и погрешности округления.

При вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления – это определяет погрешность округления.

Неустранимой  погрешностью называют погрешность, являющуюся следствием неточности задания исходных данных, входящих в математическое описание задачи.

Применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, и поэтому вместо получения точного решения задачи приходится прибегать к приближенному. Поэтому возникает погрешность метода.

Погрешность, являющуюся следствием несоответствия математического описания реальности, называют погрешностью математической модели.

Такие алгоритмы, где, вследствие ограниченности порядков чисел или малости времени, возникают недопустимые искажения результата (вычислительная погрешность), называют ”неустойчивыми”.

Построение  “устойчивых” алгоритмов, при использовании которых вычисления доводятся до конца без существенного искажения результата, составляют существенную часть теории численных методов.

Задание 2