Курсовая работа по методам вычислений
Отыскание минимума квадратичной функции – метод сопряженных градиентов
Вариант 11
Выполнил: студент II курса 217 группы Корниенко М.Ю.
Проверила: преп. Распопова Н.В.
Оценка:_________________
Санкт-Петербург
2005 г.
Оглавление
1. Постановка задачи
2. Описание метода
3. Текст программы
4. Результаты вычислений
5. Литература
3
4
5
7
8
1.Постановка задачи.
1. Изложить метод сопряженных градиентов (МСГ) для отыскания минимума квадратичной функции:
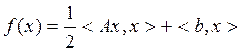 ,
(1)
,
(1)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
симметричная положительно определенная матрица,
-
симметричная положительно определенная матрица, ![]() -
скалярное произведение в
-
скалярное произведение в ![]() . Каково основное
свойство МГС?
. Каково основное
свойство МГС?
2.
Реализовать МСГ на компьютере. Критерий прекращения спуска ![]() ;
;
Продемонстрировать работу программы для:
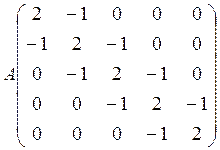 ,
, 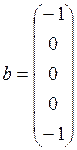 .
.
Выходные
данные программы: ![]() ,
, ![]() - номер
последнего шага, входные данные:
- номер
последнего шага, входные данные: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2.Описание метода.
Положим,
задана квадратичная функция (1) . Необходимо получить последовательность ![]() , приводящую к минимуму
, приводящую к минимуму ![]() .
.
Пусть
построены векторы ![]() ,
, ![]() и
набор
и
набор ![]() -ортогональных векторов
-ортогональных векторов ![]() . Продолжим построение по формулам:
. Продолжим построение по формулам:
![]() ,
(2)
,
(2)
причем
![]() находится из условия:
находится из условия:
![]() , т.е.
, т.е. 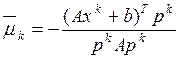 , (3)
, (3)
![]() .
(4)
.
(4)
Заметим,
что вновь построенный вектор градиента ортогонален вектору ![]() :
:
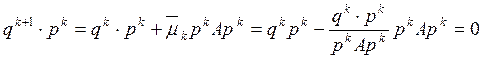 .
(5)
.
(5)
Пусть
![]() , причем
, причем ![]() ,
откуда
,
откуда 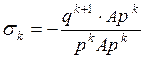 (6)
(6)
Шаг
метода закончен. В качестве начальных векторов возьмем ![]() -
произвольный вектор из
-
произвольный вектор из ![]() ,
, ![]() .
.
Лемма. Построенные последовательности обладают свойствами:
1.
![]() ,
, ![]() ;
;
2.
![]() ,
, ![]() ;
;
3.
если ![]() , то
, то ![]() ,
, ![]() ;
;
4.
![]() ;
;
5.
![]() =0,
=0, ![]() ;
;
Замечание. (О том, что отличает МСГ от остальных методов отыскания минимума) Метод сопряженных градиентов называют конечным, поскольку для квадратичной функции он за конечное число шагов приводит в точку минимума. На практике, однако, из-за погрешности вычислений число шагов может оказаться бесконечным.
Замечание.
(О практической сходимости итерационных методов) Пусть итерационный метод
таков, что имеет место оченка: ![]() ,
, ![]() и вычисления ведутся с погрешностью
и вычисления ведутся с погрешностью ![]() , причем
, причем ![]() .
.
Тогда
при прежних предположениях относительно ![]() имеет место
сходимость
имеет место
сходимость
![]() , где
, где 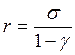 .
.
3.Текст программы
//--------------------------------------------------------------------------#include <vcl.h>
#include <conio.h>
#include <stdio.h>
#include <math.h>
long double scalarmulty(double *a,double *b,int n) //функция скалярного умножения
{
long double scm=0;
for (int i=0;i<n;i++)
scm=scm+a[i]*b[i];
return scm;
}
double *multy(double a,double *b,int n) //функция умножения вектора на число
{
double *m=new double[n];
for (int i=0;i<n;i++)
m[i]=a*b[i];
return m;
}
double *multy(double **A,double *f,int n) //функция умножения матрицы на вектор
{
double *b=new double [n]; int i,j;
for (int i=0;i<n;i++)
{
b[i]=0;
for (int j=0;j<n;j++)
b[i]=b[i]+A[i][j]*f[j];
}
return b;
}
double derivative(double **A,double *x,double *b,int n) //производная квадратичной функции
{
double der=0;
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
der=der+A[i][j]*x[j];
der=der+b[i];
}
return der;
}
double *add(double *a,double *b,int n) //функция сложения векторов
{
double *addit=new double[n];
for (int i=0;i<n;i++)
addit[i]=a[i]+b[i];
return addit;
}
float f(double **A,double *x,double *b,int n) //возвращает значение функции ф
{
double fx=0;
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
fx=fx+A[i][j]*x[j]*x[i];
fx=fx+b[i];
}
return fx;
}
#pragma hdrstop
//--------------------------------------------------------------------------#pragma argsused
int main(int argc, char* argv[])
{
double **A,*b,*xk,eps=0.0000001;
int n,i,j;
FILE *inc;
inc=fopen("input.txt","rt");
fscanf(inc,"%d",&n);
A=new double*[n]; b=new double[n];
printf("eps=%8.7f\n",eps);
for (i=0;i<n;i++)
{
A[i]=new double [n];
for (j=0;j<n;j++)
{
fscanf(inc,"%lf",&A[i][j]);
printf("%6.2lf",A[i][j]);
}
fscanf(inc,"%lf",&b[i]);
printf("%8.2f\n",b[i]);
}
xk=new double[n];
printf("\nX0: [ ");
for (i=0;i<n;i++)
{
fscanf(inc,"%lf",&xk[i]);
printf("%12.7llf",xk[i]);
}
printf("]\n");
fclose(inc);
double *TMP1,*TMP2;
double *q,*qNX,*p,*pNX;long double sigma,mu;
TMP2=multy(A,xk,n) ;
q=add(TMP2,b,n); p=add(TMP2,b,n);
delete [] TMP2;
TMP1=multy(A,p,n); mu=-scalarmulty(q,p,n)/scalarmulty(p,TMP1,n);
delete [] TMP1;
textcolor(1);
cprintf("F`(x)=%12.7lf; ",fabs(derivative(A,xk,b,n)));
textcolor(9);
cprintf("F(x)=#%lf; ",f(A,xk,b,n));
j=0;
while (fabs(derivative(A,xk,b,n))>=eps)
{
TMP1=multy(mu,p,n); TMP2=xk;
xk=add(xk,TMP1,n); j++;//x^(k+1)
delete [] TMP2;
delete [] TMP1;
TMP1=multy(A,p,n);
qNX=add(q,multy(mu,TMP1,n),n); //q^(k+1)
printf("\nX%d: [ ",j);for (i=0;i<n;i++) printf("%12.7lf",xk[i]); printf("]\n");
sigma=-scalarmulty(qNX,TMP1,n)/scalarmulty(p,TMP1,n);
pNX=add(qNX,multy(sigma,p,n),n); //p^(k+1)
delete [] TMP1;
delete [] p;p=pNX;
delete [] q;q=qNX;
TMP1=multy(A,p,n);
mu=-scalarmulty(q,p,n)/scalarmulty(p,TMP1,n); //Myu^(k+1)
delete [] TMP1;
textcolor(1);
cprintf("F`(x)=%12.7lf; ",fabs(derivative(A,xk,b,n)));
textcolor(9);
cprintf("F(x)=#%lf; ",f(A,xk,b,n));
}
getch();
return 0;
}
//--------------------------------------------------------------------------4.Результаты вычислений
При упомянутых в задании входных данных результат вычисления оказался равным:
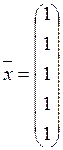 ,
, ![]() при
погрешности
при
погрешности ![]()
6.Литература
· А. П. Иванов «Методы Вычислений»
· Н.С. Бахвалов «Численные методы».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.