Изложить теоретические основы метода простых итераций (схему метода, условия сходимости и оценку погрешности) для решения системы (1). Указать типы матриц A, для которых условия сходимости можно проверить.
Обычная запись
линейной алгебраической системы такова: ![]() (1),
где
(1),
где
Матрица А
невырожденная. Для применения метода итерации система (1) должна быть приведена
к виду ![]() (2).
(2).
Итерационные методы в случае сходимости позволяют построить последовательность
![]() , такую что
, такую что ![]() при
при ![]() , где x
- решение системы
, где x
- решение системы ![]() .
.
Эти методы, как правило, имеют простую программу, и их обычно используют, когда имеется система большого порядка и точные методы работают плохо. При этом, конечно, нужно позаботиться, чтобы метод сходился. Как правило, итерационные методы работают значительно дольше точных.
Большинство
итерационных методов укладывается в следующую схему: последовательность
вектор-столбцов ![]() строится по формуле:
строится по формуле:
![]() , где
, где ![]() -
начальное приближение.
-
начальное приближение.
Методы
отличаются способом выбора матриц ![]() .
Итерационные методы можно разделить на несколько групп:
.
Итерационные методы можно разделить на несколько групп:
1) стационарные,
для которых![]() ;
;
2) циклические,
в которых матрица ![]() повторяется
через i шагов;
повторяется
через i шагов;
3) нестационарные,
где ![]() различные на каждом шаге.
различные на каждом шаге.
Из стационарных методов
часто используется метод простой итерации, в котором система ![]() записывается в виде
записывается в виде ![]() и полагают:
и полагают:
![]() , где
, где ![]() -
число.
-
число.
Необходимым и достаточным
условием сходимости является условие ![]()
для всех собственных чисел матрицы ![]() . Существуют более простые достаточные условия сходимости.
Например:
. Существуют более простые достаточные условия сходимости.
Например:
1)
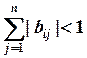 ,
, ![]() ;
;
2)
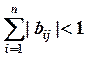 ,
, ![]() ;
;
3)
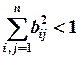 ;
;
Если метод
простой итерации не сходится для системы ![]() , то ее
можно несколько видоизменить, умножив на
, то ее
можно несколько видоизменить, умножив на ![]() обе
части системы:
обе
части системы:
![]() .
.
Матрицу ![]() выбирают так, чтобы матрица
выбирают так, чтобы матрица ![]() была близка к единичной. Такое
предварительное домножение равносильно применению стационарного метода с
матрицей
была близка к единичной. Такое
предварительное домножение равносильно применению стационарного метода с
матрицей ![]() к исходной системе. Если матрица
к исходной системе. Если матрица ![]() положительно определенная, то
положительно определенная, то ![]() можно строить так: вычислим
можно строить так: вычислим ![]() .
.
Известно, что
собственные числа матрицы ![]() не больше любой ее
нормы, поэтому
не больше любой ее
нормы, поэтому ![]() . Положим
. Положим 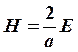 ,
тогда
,
тогда 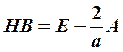 и можно доказать, что
и можно доказать, что ![]() . Это обеспечивает сходимость метода.
. Это обеспечивает сходимость метода.
Отметим
два достоинства метода итерации. Простота реализации на ЭВМ: вычисление каждого
приближения выполняется по одной и той же схеме. Из теормы о необходимом и
достаточном условии сходимости следует свойство самоисправляемости метода. Если
некоторое приближение ![]() найдется неправильно, то можно
продолжать вычисления и получить хорошее приближение к решению, если все
дальнейшие приближения вычисляются правильно. Действительно,
найдется неправильно, то можно
продолжать вычисления и получить хорошее приближение к решению, если все
дальнейшие приближения вычисляются правильно. Действительно, ![]() можно считать новым начальным
приближением.
можно считать новым начальным
приближением.
При
фактических вычислениях вопрос о сходимости метода итерации осложняется тем,
что из-за погрешностей округления мы получаем вместо последовательности ![]() другую последовательность
другую последовательность ![]() .
.
Если все
собственные значения матрицы ![]() лежат внутри единичного
круга, то может показаться, что не возникает никаких проблем относительно
поведения метода в реальных условиях ограниченности порядков чисел в машине и
присутствия округлений. В обоснование этого впечатления иногда приводят
следующий довод – возмущения приближений вследствие округлений равносильны
возмущениям начальных условий итерационного процесса. Поскольку процесс
сходящийся, “самоисправляющийся”, эти возмущения в конце концов затухнут и
будет получено хорошее приближение к решению исходной задачи.
лежат внутри единичного
круга, то может показаться, что не возникает никаких проблем относительно
поведения метода в реальных условиях ограниченности порядков чисел в машине и
присутствия округлений. В обоснование этого впечатления иногда приводят
следующий довод – возмущения приближений вследствие округлений равносильны
возмущениям начальных условий итерационного процесса. Поскольку процесс
сходящийся, “самоисправляющийся”, эти возмущения в конце концов затухнут и
будет получено хорошее приближение к решению исходной задачи.
Однако при
решении некоторых систем возникала следующая ситуация. Все собственные значения
матрицы ![]() лежали в круге
лежали в круге 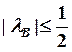 , а
итерационный процесс останавливался после некоторого числа итераций по причине
переполнения порядков чисел в ЭВМ. В других случаях такого переполнения не
происходило, но векторы
, а
итерационный процесс останавливался после некоторого числа итераций по причине
переполнения порядков чисел в ЭВМ. В других случаях такого переполнения не
происходило, но векторы ![]() , получаемые при
вычислениях, не имели тенденции к установлению. Последний случай наиболее
опасен. Суммарная вычислительная погрешность может оказаться большой не только
из-за большой величины отдельных слагаемых, но и из-за того, что их много.
Погрешность порядка
, получаемые при
вычислениях, не имели тенденции к установлению. Последний случай наиболее
опасен. Суммарная вычислительная погрешность может оказаться большой не только
из-за большой величины отдельных слагаемых, но и из-за того, что их много.
Погрешность порядка ![]() является неустранимой и
возмущение приближений, создаваемое в ходе итераций, сравнимо с неустранимой
погрешностью. С целью уменьшения числа итераций при переходе к системе
является неустранимой и
возмущение приближений, создаваемое в ходе итераций, сравнимо с неустранимой
погрешностью. С целью уменьшения числа итераций при переходе к системе ![]() стараются получить систему с возможно
меньшим значением
стараются получить систему с возможно
меньшим значением ![]() ; поэтому можно привести довольно
мало примеров решения задач, где
; поэтому можно привести довольно
мало примеров решения задач, где ![]() , например, больше
0.9999.
, например, больше
0.9999.
Задание 3
Составить и отладить программу, реализующую указанный в задании 2 метод с требуемой точностью. Продемонстрировать ее работу на примере системы (1) с
A= 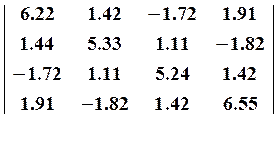
C= 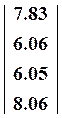
Текст программы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.