Практикум по численным методам
Отчет
Интерполирование функций
студентка:
Кирушева И.В., 319гр.
преподаватель:
Остов Ю.Я.
Факультет ПМ-ПУ СПбГУ 2007
1. Постановка задачи:
Для функции ![]() выполнить следующее:
выполнить следующее:
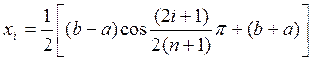
2 Решение задачи
2.1 Выбор интервала непрерывности
Построим график функции ![]() :
:
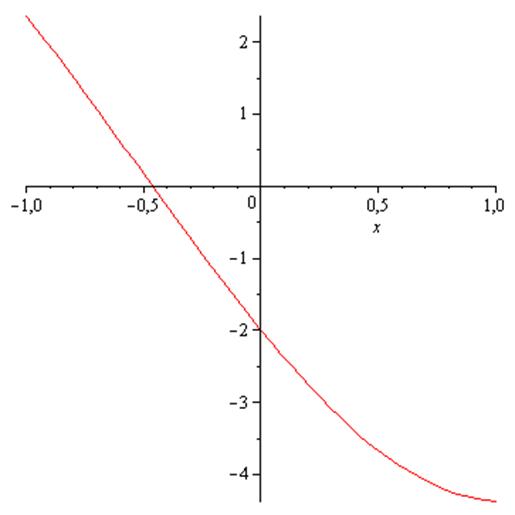
В качестве интервала непрерывности выберем [-1, 1] В дальнейшем данную функцию будем рассматривать только на этом отрезке.
2.2 Код программы
Алгоритм построения интерполяционного полинома Лагранжа реализован на языке программирования встроенном в систему Maple. Код программы:
В начале программы задаются исходные данные алгоритма, далее строится полином Лагранжа. В итоге получаем графики интерполяционных функций для обоих способов выбора
> Digits:=5:
> f:=x->x^2-2-4*sin(x);
> ![]()
n := 3;
> ![]()
a:=-1; b:=1;
> X11 = array(1..n):
> ![]()
for i from 1 to n do
X11[i]:= ((b-a)/(n-1))*(i-1)+a;
end do;
![]()
![]()
![]()
![]()
> w:=proc(x, X)
r:=1:
for i from 1 to n do
r:=r*(x-X[i]):
end do:
end proc:
> l:=proc(i,x, X)
w(x, X)/((x-X[i])*eval(diff(w(t, X), t), t=X[i]))
end proc:
> P11:=0;
>
for k from 1 to n do
P11:=P11+l(k, x, X11)*f(X11[k]):
end do:
> ![]()
simplify(P11);
![]()
> X21 = array(1..n):
> 
for i from 1 to n do
X21[i]:= 0.5*((a-b)*cos((2*(i-1)+1)*Pi/(2*n))+(a+b));
end do;
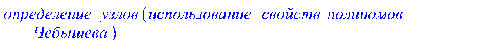
![]()
![]()
![]()
> P21:=0;
![]()
> for k from 1 to n do
P21:=P21+l(k, x, X21)*f(X21[k]):
end do:
> ![]()
simplify(P21);
![]()
> ![]()
n:=7:
> X12 = array(1..n):
> ![]()
for i from 1 to n do
X12[i]:= ((b-a)/(n-1))*(i-1)+a;
end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> P12:=0;
> for k from 1 to n do
P12:=P12+l(k, x, X12)*f(X12[k]):
end do:
> ![]()
simplify(P12);
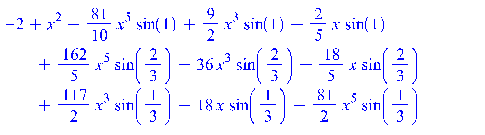
> X22 = array(1..n):
> 
for i from 1 to n do
X22[i]:= 0.5*((a-b)*cos((2*(i-1)+1)*Pi/(2*n))+(a+b));
end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> P22:=0;
> for k from 1 to n do
P22:=P22+l(k, x, X22)*f(X22[k]):
end do:
> ![]()
simplify(P22);
![]()
3 Результаты работы программы:
На графиках черной линией будем обозначать график исходной функции, а синей и красной - графики интерполяционных функций (узлы задаются двумя разными способами)
Рассмотрим случай с 3 узлами интерполяционной сетки:
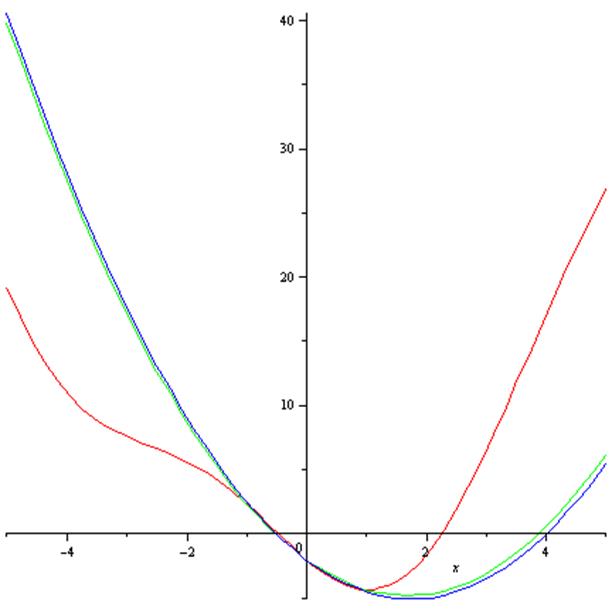
А теперь с 7 узлами:
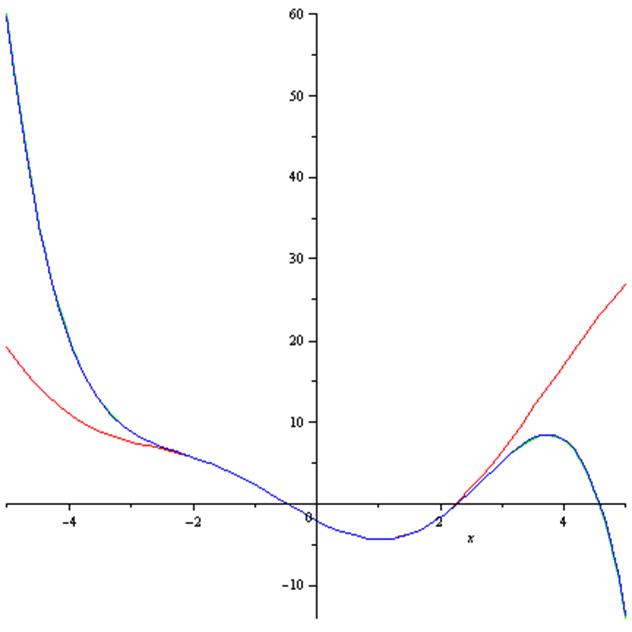
Из графиков функций видно, что во втором случае достигается более точное приближение к исходной функции.
Список литературы:
1. А.П.Иванов Методические указания Тема 5: Интерполирование функций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.