Санкт-Петербургский государственный Университет.
Факультет Прикладной Математики – Процессов Управления
Курсовая работа по Методам Вычислений
Вычисление определенного интеграла
(вариант 12)
Исполнитель:
студентка 28 группы
Кутявина К.А.
Руководитель:
доцент Матросов А.В.
2004 г.
Задание
1. Привести составную квадратурную формулу трапеций (СКФТ) для приближенного вычисления определенного интеграла. Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.
2. Составить программу, реализующую данный метод с заданной точностью.
Входные
данные программы : n – начальное число узлов, m – предельное число узлов, ![]() - точность;
- точность;
Выходные данные : Sk – приближенное значение интеграла, k – число узлов,обеспечивающее заданную точность вычисления интеграла.
3.
Вычислить : I = 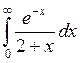 с точностью
с точностью ![]() = 10-4
= 10-4
Выполнение задания
Представим исходный интеграл в виде I =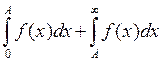 , причем число A выберем так, чтобы выполнялось неравенство
, причем число A выберем так, чтобы выполнялось неравенство 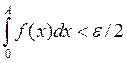 . Подберем функцию
. Подберем функцию ![]() :
:
![]() ; вычислим интеграл
; вычислим интеграл 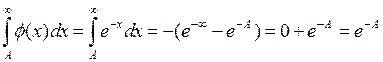 ,
найдем А из условия:
,
найдем А из условия: ![]() ,
, ![]()
учитывая
данное значение ![]() =10-4, получаем, что в
качестве А можно взять например число ln(105) = 5 ln(10)
= A.
=10-4, получаем, что в
качестве А можно взять например число ln(105) = 5 ln(10)
= A.
Таким образом, приходим к задаче вычисления определенного интеграла 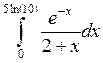 .
.
Приведём составную квадратурную формулу трапеций с остаточным членом.
Пусть f ÎС2[а,b],
f i+1/2 = f (a +i*h), i= 0, 1, ...,
N—1, h=(b—a)/N, ![]() Î[a, b] — некоторая точка. Имеем:
Î[a, b] — некоторая точка. Имеем:
|
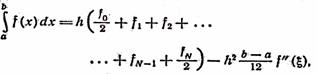 |
![]()
где cне зависит от h; k = 2 для формулы трапеций
Предполагается, что fÎС2+k[а,b].
Вычислив Ih*2, Ih, Ih/2 и убедившись, что 2k(Ih–Ih/2)/(Ih*2–Ih) близка к единице, можно приблизительно оценить погрешность I–Ih/2 по правилу Рунге:
I–Ih/2 =(Ih/2–Ih)/(2k-1)
В
нашем случае оценка погрешности примет вид : ![]()
Программа, реализующая метод для данного интеграла с учетом заданной погрешность ( на Delphi.6)
unit U1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Button1: TButton;
Button2: TButton;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Label3: TLabel;
Label4: TLabel;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
function fun(x:real):real; //вычисление значения подынтегральной функции
begin
fun:= exp(-x)/(2+x);
end;
procedure TForm1.Button1Click(Sender: TObject);
var n,m,j,i,k,t:integer;
var A,Ih,Io,h,Ist,eps :real;
begin
n:=strtoint(edit1.text)-1; // начальное кол-во узлов
m:=strtoint(edit2.text)-1; // предельное кол-во узлов
eps:= exp(-4*ln(10)); //погрешность вычислений
A:=exp(5*ln(10)); //верхняя граница интегрирования, определенная по указанному правилу
Io:=0;
k:=trunc((ln(m/n))/(ln(2))); //вспомогательная перменная
for j:=0 to k do
begin
h:=A/(exp(j*ln(2))*n); //шаг дробления
Ih:=0;
for i:= 0 to round(exp(j*ln(2))*n - 1) do //вычисление интеграла на данном дроблении
Ih:=Ih+ h*(fun(i*h)+fun((i+1)*h))/2;
Ist:=Ih;
if abs(Ist - Io)< 3*eps/2 then break //проверка погрешности по правилу Рунге
else Io:=Ist //переобзначение для продолжения циклического процесса end;
edit4.Text:=floattostr(exp(j*ln(2))*n +1); //конечное количество узлов
edit3.Text:=floattostr(Ist); //значение интеграла
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
close; // выход из программы
end;
end.
Результаты работы приведенной программы
|
Начальное кол-во узлов |
Предельное кол-во узлов |
Искомое кол-во узлов |
Значение интеграла |
|
105 |
106 |
159998 |
0,3623043952 |
|
107 |
|
2 |
0,361330179 |
|
108 |
|
|
0,3613286325 |
выходные данные
Исходный интеграл для проверки был посчитан также и с помощью прикладного пакета «Математика».
Результат
вычисления : I = 0.3613286169. В таблице результатов при последней
попытке вычисления результат совпадает с I с
точностью порядка 10-8 < ![]() .
. ![]()
В
программе рассмотрен случай половинного деления каждого промежутка при
совершении одного «шага». Таким образом, деление отрезка ![]() происходит лишь добавлением узловых точек
на каждом шаге (промежутков становится в 2 раза больше, чем на
предыдущем ) ,а не новым дроблением с добавлением лишь одной узловой
точки.
происходит лишь добавлением узловых точек
на каждом шаге (промежутков становится в 2 раза больше, чем на
предыдущем ) ,а не новым дроблением с добавлением лишь одной узловой
точки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.