Нечеткая реализация скользящих режимов в системе возбуждения синхронного генератора (В.Д. Бобко, Ю.Н. Золотухин, А.А. Нестеров)

НЕЧЕТКАЯ РЕАЛИЗАЦИЯ СКОЛЬЗЯЩИХ РЕЖИМОВ В СИСТЕМЕ ВОЗБУЖДЕНИЯ СИНХРОННОГО ГЕНЕРАТОРА

В.Д. Бобко,  Ю.Н. Золотухин,  А.А. Нестеров.

Лаборатория нечетких технологий

Институт автоматики и электрометрии

Сибирское отделение РАН

630090  Новосибирск,  просп. ак. Коптюга, 1

Россия

Тел.: (3832) 33 26 25, Факс: (3832) 33 38 63

E-mail: zol@idisys.iae.nsk.su

Ключевые слова: нечеткое управление, скользящий режим, динамическая устойчивость энергосистем

Abstract

This paper presents a fuzzy implementation of slide mode control to improve of power

system stability

Проблема обеспечения стабильной работы синхронных генераторов в энергосистеме остается актуальной, несмотря на создание и использование сильных регуляторов возбуждения. Причина в том, что линейный регулятор не может удовлетворительно функционировать ( без перестройки параметров ) при значительных изменениях режимов работы энергосистемы, особенно при возникновении аварийных ситуаций. Одним из путей преодоления указанных трудностей является организация в системе скользящих режимов [1]. При этом рабочая точка системы скользит вдоль заданных поверхностей, что обеспечивает удовлетворительное качество процессов при значительных изменениях параметров системы. Нужно отметить, что осуществление скользящих режимов требует реализации существенно нелинейных законов управления, в связи с чем представляется перспективным управление "по правилам" в пространстве состояний с помощью нечетких контроллеров.

В [2] рассмотрена задача стабилизации системы первичный двигатель - синхронный генератор - линия электропередачи с помощью дополнительных воздействий на регулятор скорости первичного двигателя и регулятор возбуждения, формируемых нечетким контроллером. Однако при формировании скользящего режима в [2] учитывается только необходимость подавления колебаний ротора генератора и не учитываются колебания напряжения на его шинах. Кроме того желаемая траектория движения ротора описана уравнением первого порядка, что не позволяет непосредственно учесть роль дополнительных стабилизирующих воздействий и делает формирование алгоритма функционирования нечеткого контроллера затруднительным. Для формирования правил необходим анализ процессов, происходящих в генераторе.

Для их анализа воспользуемся уравнениями Парка - Горева. Все уравнения будем записывать в относительных единицах. Пренебрегаем э.д.с. трансформации, активными сопротивлениями статора и линии электропередачи и малыми отклонениями частоты от синхронной. Введем векторы потокосцепления и тока

где

потокосцепления и токи статора по осям d и q соответственно ,

  потокосцепления и токи обмотки возбуждения и успокоительных обмоток по осям d и q соответственно. Токи и потокосцепления связаны соотношением

(1) где L - матрица собственных и взаимных реактивностей генератора. Напряжения генератора определяются следующими уравнениями:

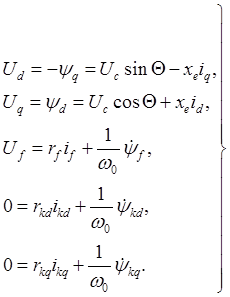
                                                                                      (2)

Здесь Ud и Uq - проекции напряжения на шинах генератора на оси d и q соответственно, Uf - напряжение возбуждения, Uc - напряжение сети бесконечной мощности,   - угол между продольной осью ротора ( осью d ) и вектором напряжения сети бесконечной мощности Uс, xe- реактивное сопротивление линии, rf, rkd, rkq - сопротивления обмотки возбуждения, продольной и поперечной успокоительных обмоток соответственно. Движение ротора описывается уравнением

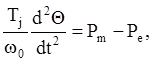
(3) где Tj - постоянная времени, характеризующая инерцию ротора и первичного двигателя, Pm - мощность первичного двигателя, Pe - электрическая мощность генератора,

                 .                                                                       (4) Для полного описания системы необходимо добавить уравнения регуляторов напряжения генератора и скорости первичного двигателя. Обозначим через Ua и Um дополнительные сигналы, предназначенные для стабилизации системы. Уравнения регуляторов запишем в следующем виде:

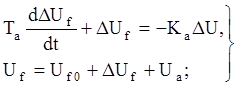
(5)

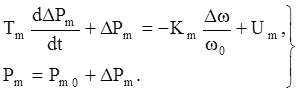
                                                                                                                                         (6) Здесь             отклонения от номинальных значений напряжения и частоты соответственно,Uf0 и Pm0 - заданные номинальные значения Uf и Pm. Следует обратить внимание на то, что сигнал Ua подается непосредственно на обмотку возбуждения, а Um - на регулятор скорости первичного двигателя.

Сигналами Ua и Um следует распорядиться таким образом, чтобы система была устойчива и имела удовлетворительные переходные процессы.

Желаемую траекторию зададим двумя уравнениями

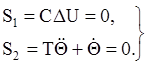
                                                                                         (7) Выполнение двух условий (7) можно заменить выполнением условия