Решение задачи аналитического конструирования оптимального регулятора и получение оптимального управления для заданного объекта по заданному критерию оптимальности с помощью метода динамического программирования

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматики

Расчетно-графическая работа №2

по курсу

«Системы автоматической оптимизации»

Факультет:         АВТ

Группа:               ААМ-10

Студент:             Барташ Б. А.                                                             Преподаватель:

Французова Г. А. 

Вариант: 3         

Дата выполнения:

Отметка о защите:

Новосибирск, 2010

Задание

Рассчитать оптимальное управление для объекта, математическая модель которого имеет вид:

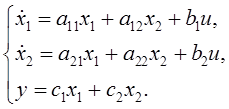
Известны ограничение на управляющее воздействия, , начальная  и конечная точки . Заданы требования к качеству процесса в виде критерия оптимальности 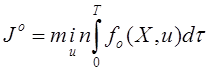 и длительности процесса .

Численные значения параметров представлены в таблице 1.

Таблица 1.

0	1	-2	-3	0	5	2	1	4	0			2

Решение

В соответствии с исходными данными математическая модель объекта будет иметь вид:

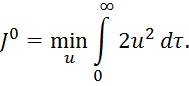
Для расчета регулятора воспользуемся методом динамического программирования.

Расчетные соотношения метода:

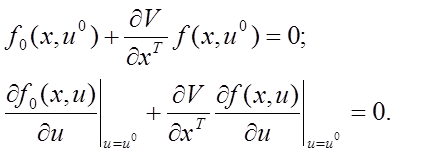
Исходя из этих соотношений, запишем уравнения для нашей системы:

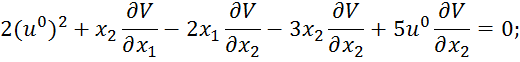
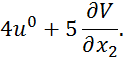
Из второго уравнения найдем оптимальное управление

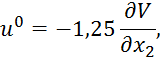
И подставим в первое уравнение:

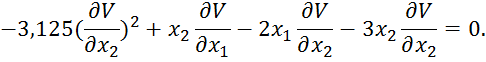
Нужно решить это уравнение при граничном условии V(x(T)) = 0. Решение будем искать в квадратичной форме:

Подставляя это выражение в уравнение Беллмана, получим:

Или

Последнее равенство тождественно, если

Система имеет несколько наборов решений:

Таким образом, получаем три варианта оптимального управления:

Из них только второй закон управления обеспечивает устойчивый переходный процесс:

Выводы

С помощью метода динамического программирования решена задача аналитического конструирования оптимального регулятора и получено оптимальное управление для заданного объекта по заданному критерию оптимальности.